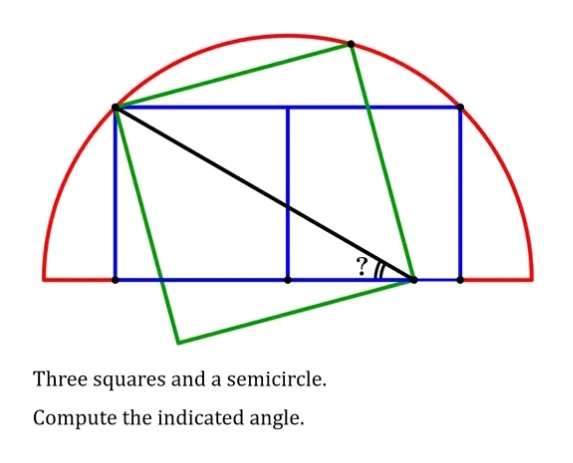
Mathematics Question and Solution
Let the side length of the inscribed two blue squares be 1 unit.
a² = 2(1)²
a = √(2) units.
a is the radius of the green half circle.
b = a-1
b = (√(2)-1) units.
tanc = 1/(√(2)-1)
c = atan(1/(√(2)-1))°
c = 67.5°
d = 90-c
d = 22.5°
Notice!
The side length of the green square is equal the radius of the red half circle.
Therefore;
e = a = √(2) units.
e is the side length of the green square.
f² = 2e²
f² = 2√(2)²
f = √(4)
f = 2 units.
f is the black diagonal length of the green square.
Therefore, the required angle, ?, let it be g is;
sing = 1/f
1 is the given length of the blue side length.
sing = 1/2
g = asin(½)
g = 30°
Again, g is the required angle ?
Or
The required angle, ? is;
The radius two radius of the circle will make an equilateral triangle with the top side length of the green square.
Therefore;
h = 90-60 = 30°
Notice, the radius of the circle again will make an isosceles triangle with a side length of the green square.
j = ½(180-30)
j = 75°
j is the two equal interior angles of the formed isosceles triangle.
Again, the black diagonal length of the green square cuts one of the equal interior angles of the isosceles triangle at half 90° (45°).
It implies, the required angle, ? is;
? = 75-45
? = 30°