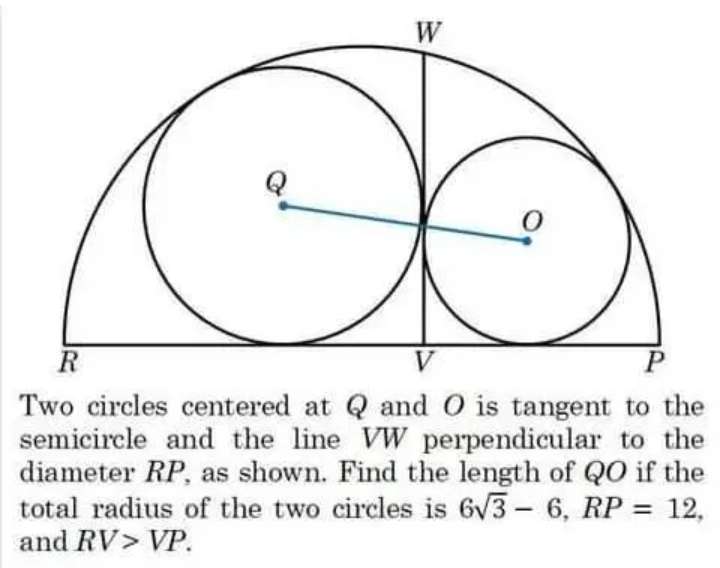
Mathematics Question and Solution
Let R=the bigger inscribed circle radius.
Let r=the smaller inscribed circle radius.
It implies;
R+r=6√(3)-6=4.4
R+r=4.4 -------(1).
And the radius of the ascribed semi circle is 6 unit.
Calculating the R and r considering the radius of the ascribed semi circle.
R=√((6-R)²-R²)
Therefore;
R=√(36-12R) ----- (2).
r=√((6-R)²-R²)
Therefore;
r=√(36-12r) ----- (3).
Adding (2) and (3).
R+r=√(36-12R)+√(36-12r)-----(4)
Therefore equating (1) and (4).
√(36-12R)+√(36-12r)=4.4------(5)
At (1).
R=4.4-r -------(6).
Substituting (6) in (5).
√(36-12(4.4-r))+√(36-12r)=4.4
Therefore;
4.4=√(36-52.8-12r)+√(36-12r)
4.4=√(12r-16.8)+√(36-12r)
4.4-√(12r-16.8)=√(36-12r)
(4.4-√(12r-16.8))²=36-12r
19.36-8.8√(12r-16.8)+12r-16.8=36-12r
2.56-8.8√(12r-16.8)=36-24r
24r-33.44=8.8√(12r-16.8)
(24r-33.44)²=8.8²(12r-16.8)
576r²-1605.12r+1118.23=929.28r-1301
576r²-2534.4r+2419.23=0
Using a quadratic equation app to resolve the above quadratic equation, it implies
r≠2.99997
r=1.40003≈1.4 unit.
Calculating R, using (6).
R=4.4-r, and r=1.4
Therefore;
R=3 unit.
Length QO will be;
√((4.4)²+(3-1.4)²
=√(4.4²+1.6²)
=√(21.92)
QO = 4.68187996429 unit.