Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
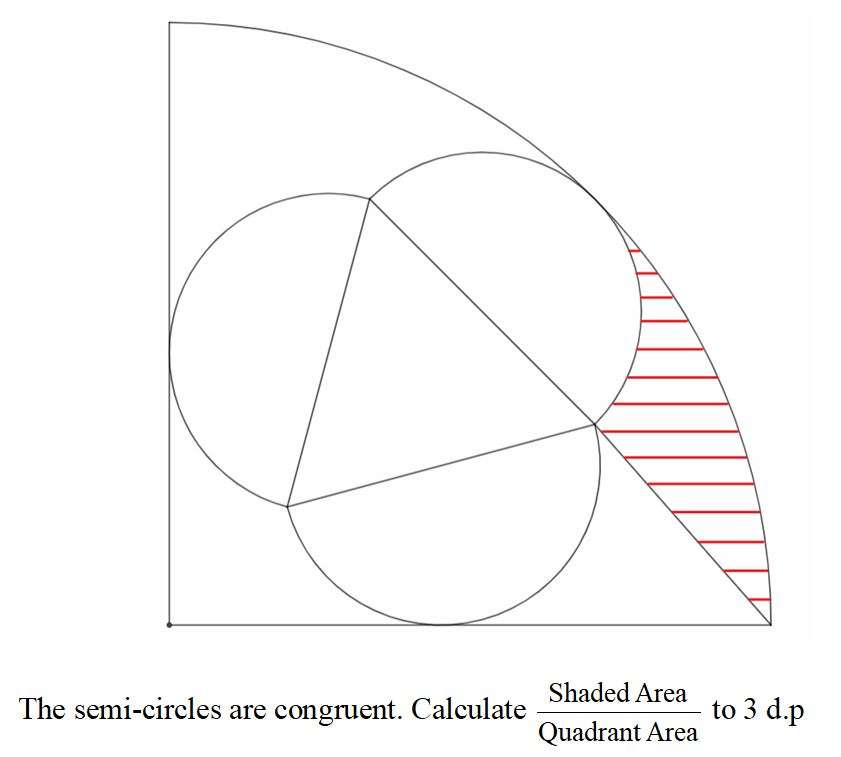
Let the radius of the ascribed quarter circle be 2 units.
Area Quadrant is;
¼(4)π
= π square units.
The radius, r of the congruent inscribed semi-circles is;
2r+√(3)r = 2
r = 2/(2+√(3)) units.
r = 0.53589838486 units.
a = 2r
a = 1.07179676972 units.
b² = 1.07179676972²+0.53589838486²-0.53589838486*2*1.07179676972cos150
b = 1.55909609015 units.
(1.55909609015/sin150) = (1.07179676972/sinc)
c = 20.10390936081°
d = 45-c
d = 24.89609063919°
e = 2-r
e = 1.46410161514 units.
It implies;
Area Shaded is;
Half Area Quadrant - Area Quadrant with radius 0.53589838486 unit - Area triangle with height 0.53589838486 unit and base 1.46410161514 units - Area triangle with height 1.55909609015 units and base 2sin24.89609063919.
½(π) - 0.22555620432 - 0.39230484541 - 0.65633879845
= 0.29659647861 square units.
Therefore;
Areas Shaded ÷ Area Quadrant to 3 decimal places is;
0.29659647861 ÷ π
= 0.09440959135
≈ 0.094