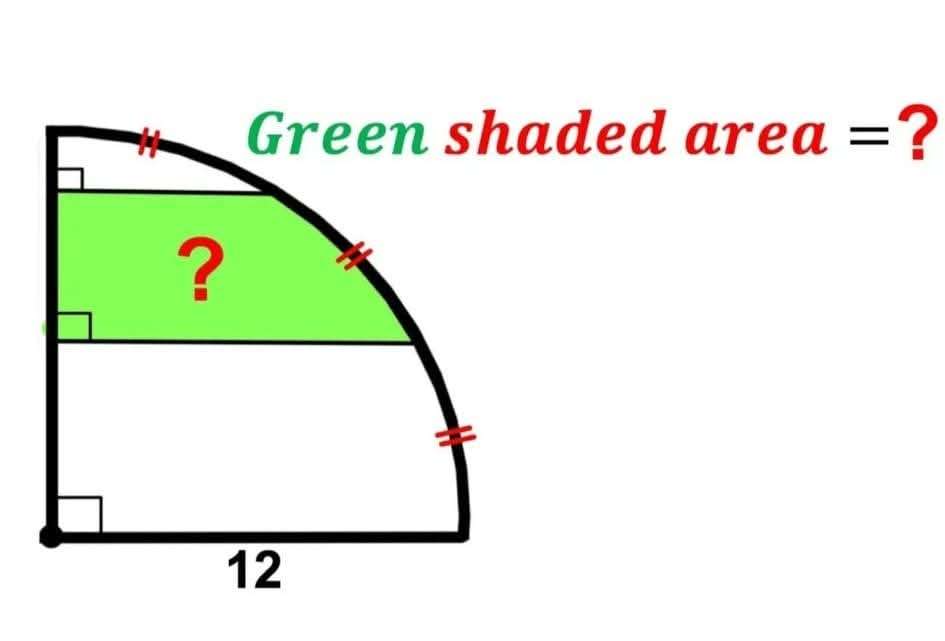
Mathematics Question and Solution
Calculating Area Green.
sin30 = a/12
a = 6 units.
b²+6² = 12².
b = √(144-36)
b √(108)
b = 6√(3) units.
sin60 = c/12
c = 6√(3) units.
d² = 12²-(6√(3))²
d = √(144-108)
d = √(36)
d = 6 units.
Therefore, green area is;
(60π*12²/360)-(30π*12²/360)
= 24π-12π
= 12π square units.
Another Approach is;
Area green is;
Area trapezoid with parallel lengths 6√(3) units and 6 units, and height (6√(3)+6) units+Area second with radius 12 units and angle 30°-Area triangle with height 12 units and base 12sin30 units.
(½(6√(3)+6)*(6√(3)-6))+(30π*12²/60)-(½*12²sin30)
= ½(72)+(12π)-36
= 36+12π-36
= 12π square units.