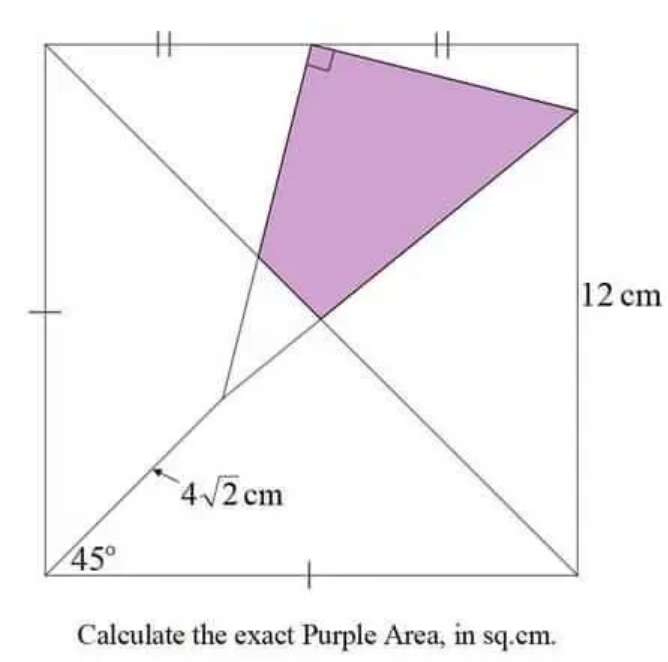
Sir Mike Ambrose is the author of the question.
The vertices of area purple is;
(6, 12) ((24/5), (36/5)) ((180/29), (168/29)) (12, (21/2))
Area purple is;
½((6, 12) ((24/5), (36/5)) ((180/2...
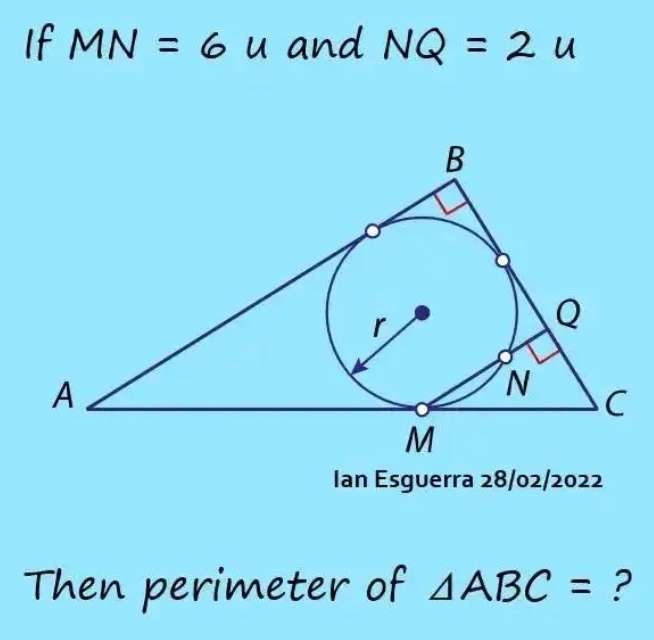
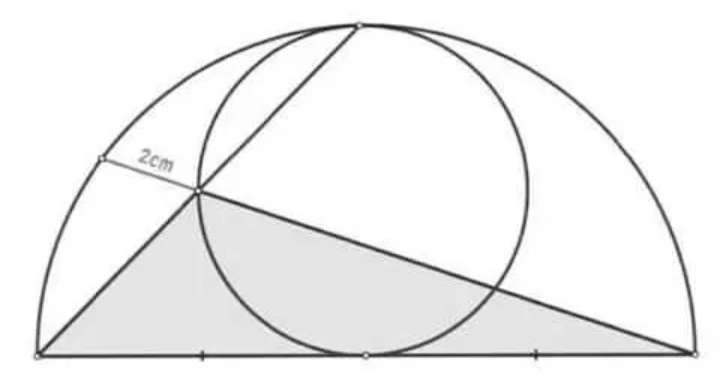
Notice.
MN = CQ = 6 units.
MQ = 6+2
MQ = 8 units.
a² = 8²+6²
a = √(100)
a = 10 units.
a is CM.
3 - 6
r - 10
Cross Multiply.
6r = 30
r = 5 units.
r is the radius of the insc...
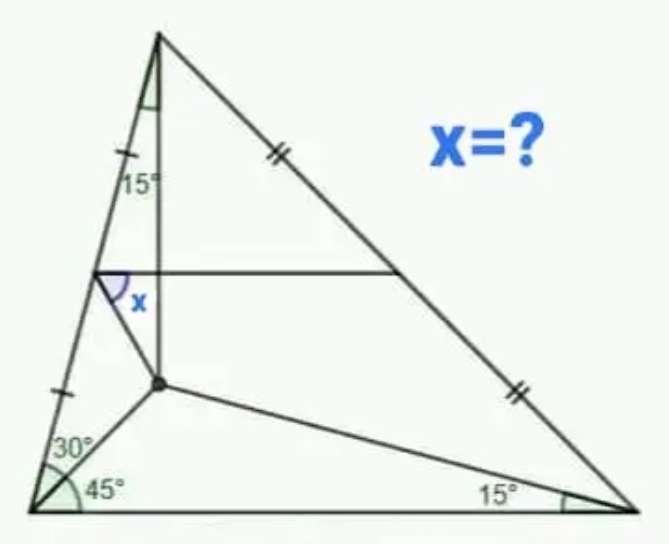
Calculating x.
Let the base of the ascribed triangle be 1 unit.
a = 180-15-45
a = 120°
(1/sin120) = (b/sin15)
b = 0.2988584907 units.
c = 180-15-30
c = 135°
(0.2988584907/sin15) =...
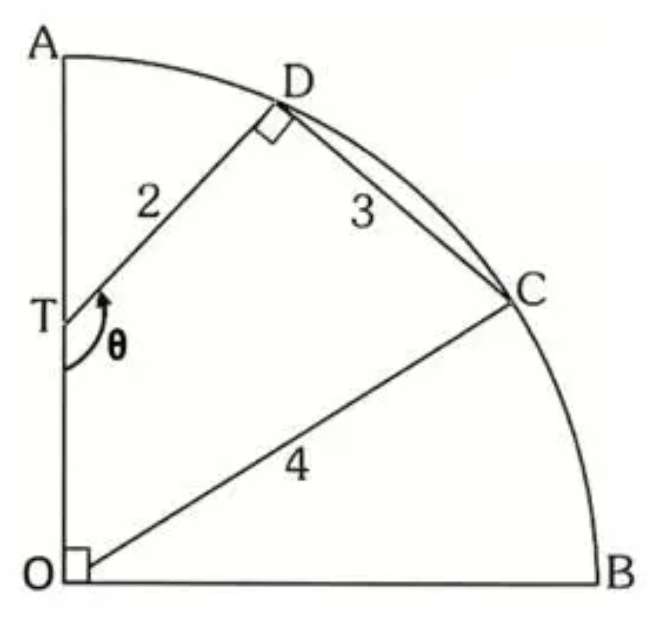
Notice.
Calculating the required angle, alpha.
4 units is the radius of the quarter circle.
It implies;
3² = 4²+4²-2*4*4cosa
9 = 32-32cosa
32cosa = 32-9
a = acos(23/32)
a = 44.04862...
Calculating Area Shaded.
Let r be the radius of the semi circle.
Calculating r.
((6r/√(10))-2)²=(r/2)²+(3r/2)²
72r²-48√(10)r+80=50r²
22r²-48√(10)r+80= 0
11r²-2⁴√(10)r+40= 0
Therefore...
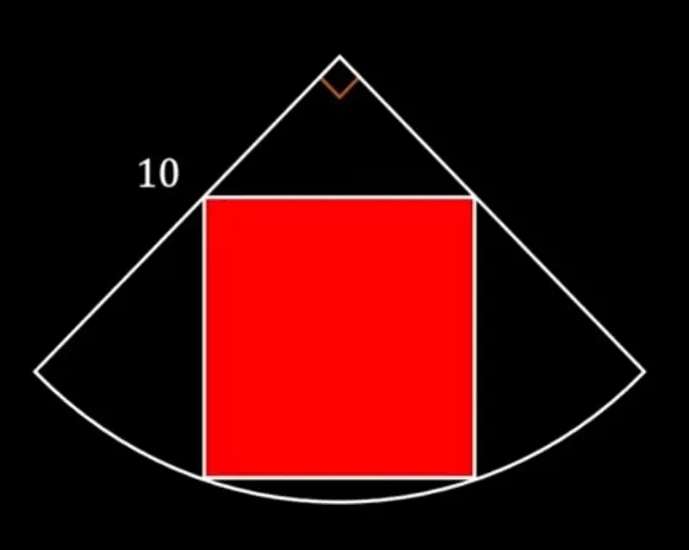
Calculating area of the inscribed red square.
Let a be the side length of the inscribed red square.
2b² = a²
b = √(a²/2)
b = ½√(2)a units.
10² = a²+(½√(2)a)²-2a*½√(2)acos(45+90)
100 = ½...
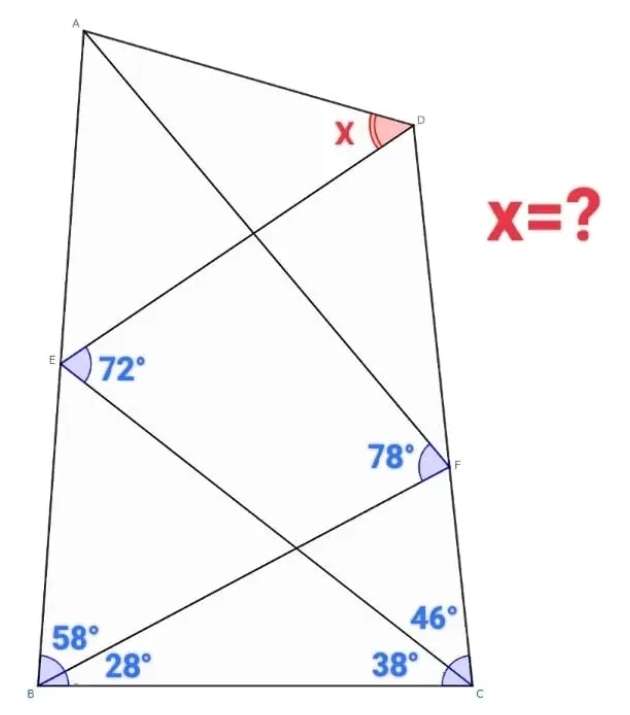
Let the base of the quadrilateral be 1 unit.
a = 180-58-28-38
a = 180-124
a = 56°
(1/sin56) = (b/sin(58+28))
b = 1.2032796622 units.
(1/sin56) = (c/sin38)
c = 0.7426219217 units.
d...
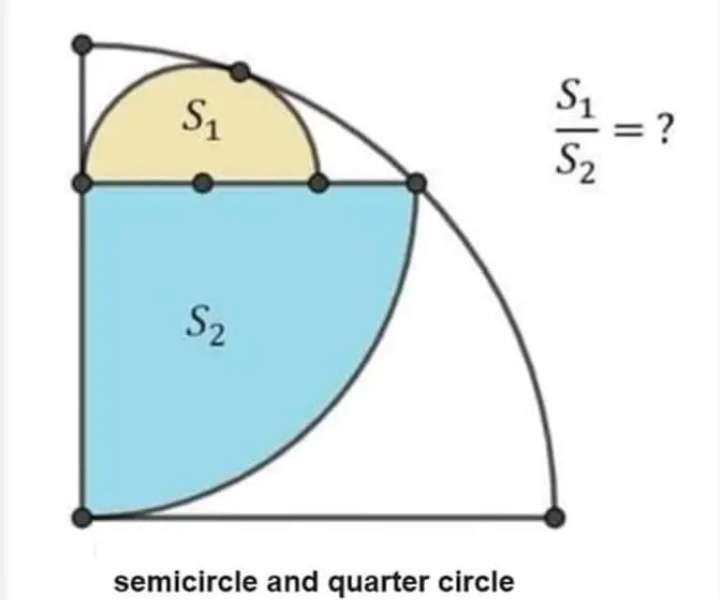
Let the ascribed quarter circle radius be 1 unit.
2a² = 1²
a² = ½
a = ½√(2) units.
a = 0.7071067812 units.
a is the radius of the blue inscribed quarter circle.
Area blue inscribed quarte...
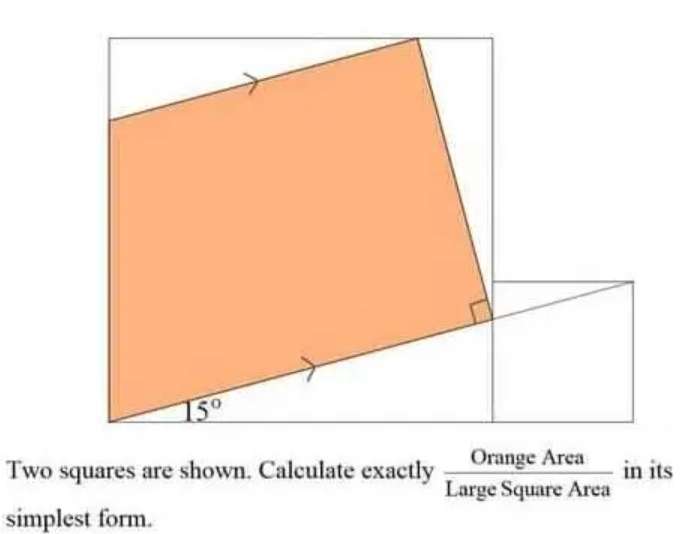
Sir Mike Ambrose is the author of the question.
Let the single side length of the small square be 1 unit.
Therefore;
Area large square is;
((1/tan15)-1)²
= 7.46410161514 square units....
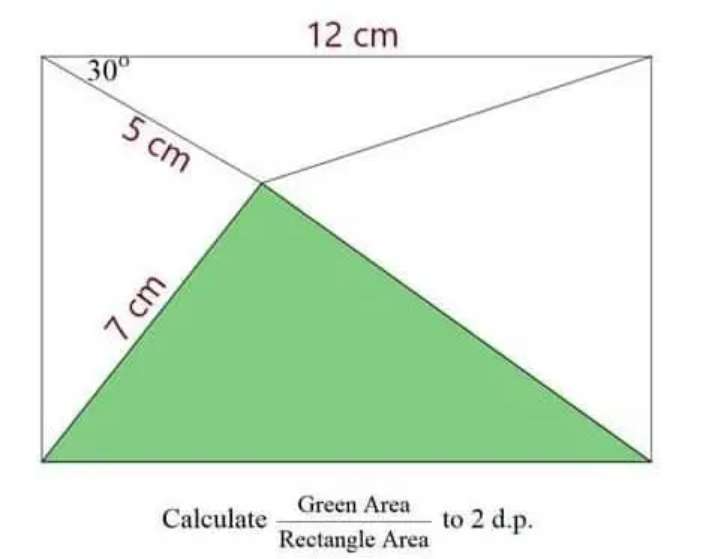
Sir Mike Ambrose is the author of the question.
The width of the rectangle is;
(5/2)+(11/2)
= 8 cm
Area Rectangle is;
12*8 = 96 cm²
Area Green is;
½(7*12)sin((90-atan(5√(3)/11)))...