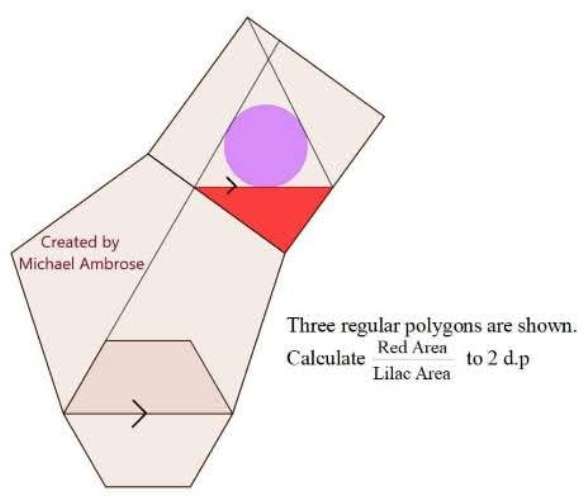
Let the side of the regular pentagon be 1 unit.
Calculating Area Red.
a² = 1²+1²-2*1*1cos108
a = 1.61803398875 units.
b = 108-36-60
b = 12°
(c/sin12) = (1.61803398875/sin96)
c = 0.33...
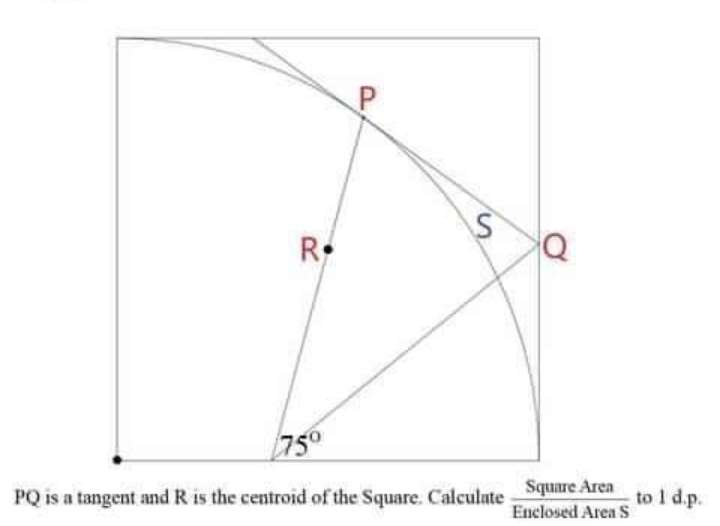
Sir Mike Ambrose is the author of the question.
Let the side of the square be 2 units.
Therefore;
Area square is;
2²
= 4 square units.
Area S is;
Area triangle with two side 0.9892...
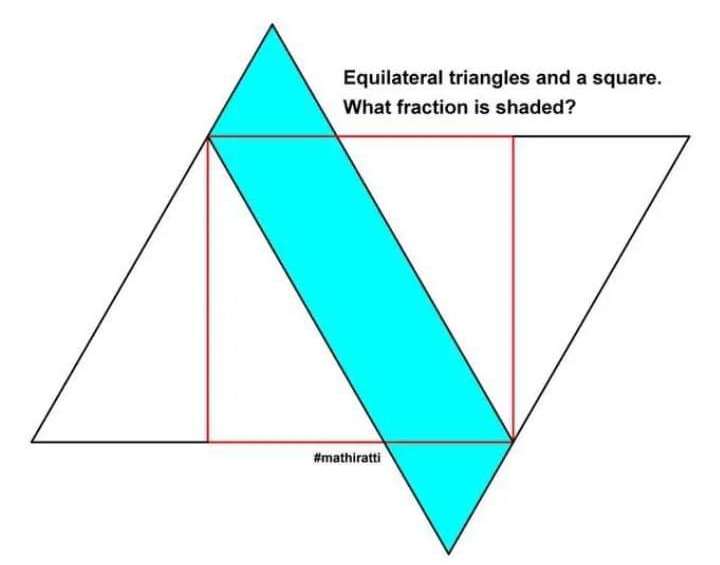
Let the square side be 2 units.
tan30 = a/2
a = ⅓(2√(3)) unit.
sin60 = 2/b
b = ⅓(4√(3)) units.
c = 2-a
c = ⅓(6-2√(3)) units.
It implies;
Area Shaded is;
2(½*(⅓(6-2√(3)))²sin60)...
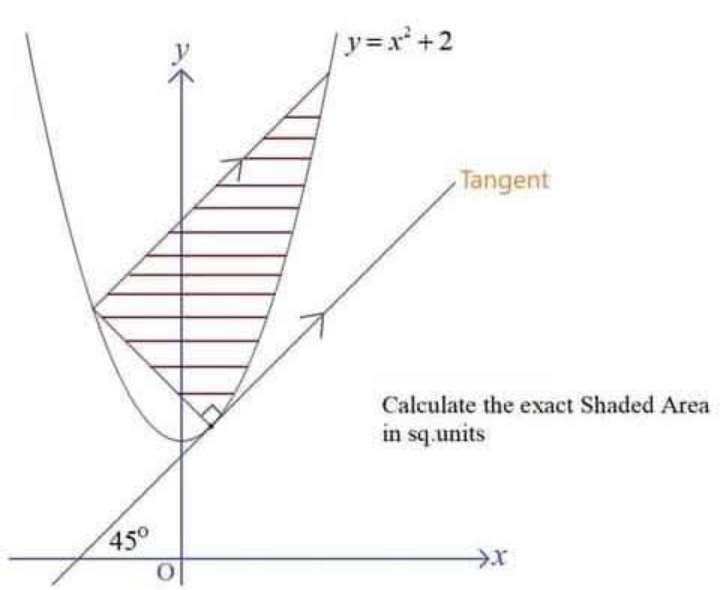
Sir Mike Ambrose is the author of the question.
Shaded area coordinates are;
Coordinate X is;
X(½, (9/4))
Coordinate Y is;
Y((-3/2), (17/4))
Coordinate Z is;
Z((5/2), (33/4))...
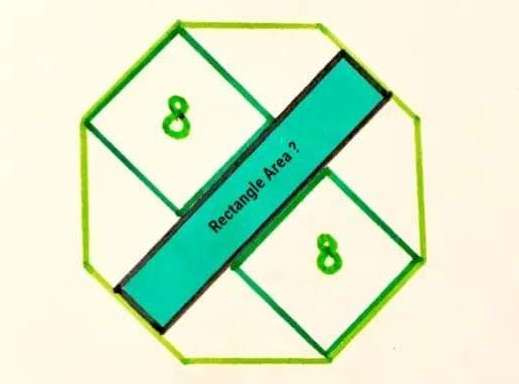
Let the side of the regular octagon be a.
Calculating a.
a² = 8
a = √(8)
a = 2√(2) units.
2b² = (2√(2))²
b = 2 units.
c = 2√(2)+2+2
c = (2√(2)+4) units.
Where c is the length of...
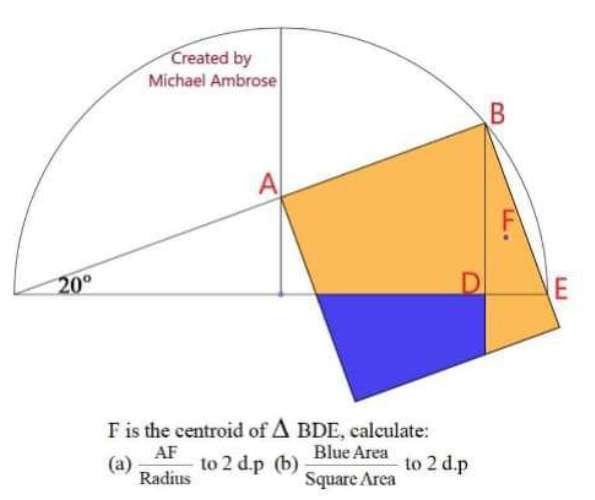
Sir Mike Ambrose is the author of the question.
Let the radius of the semi circle be 1 unit.
cos20 = a/2
a = 1.87938524157 units.
cos20 = 1/b
b = 1.06417777248 units.
c = a-b
c = 0.815...
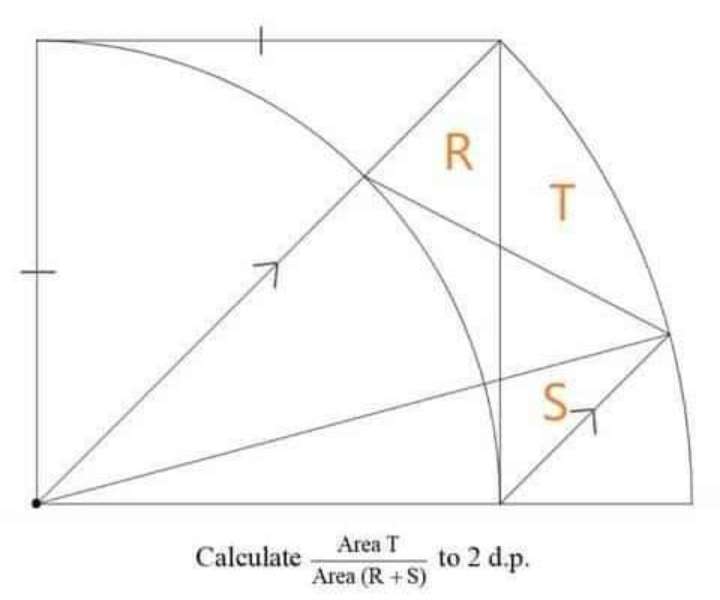
Sir Mike Ambrose is the author of the question.
Let the side of the inscribed square be 2 units.
Therefore;
Area S is;
Area triangle with two side 1.03528 units and 0.53589838486 units, a...
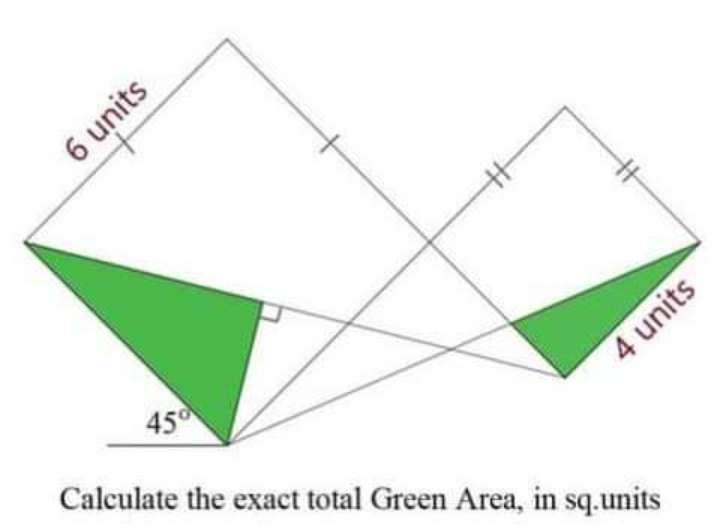
Sir Mike Ambrose is the author of the question.
Area green total, in square unit decimal form is;
Area triangle with height 6sin(atan(3/5)) units and base 6cos(atan(3/5)) units + Area triangle...
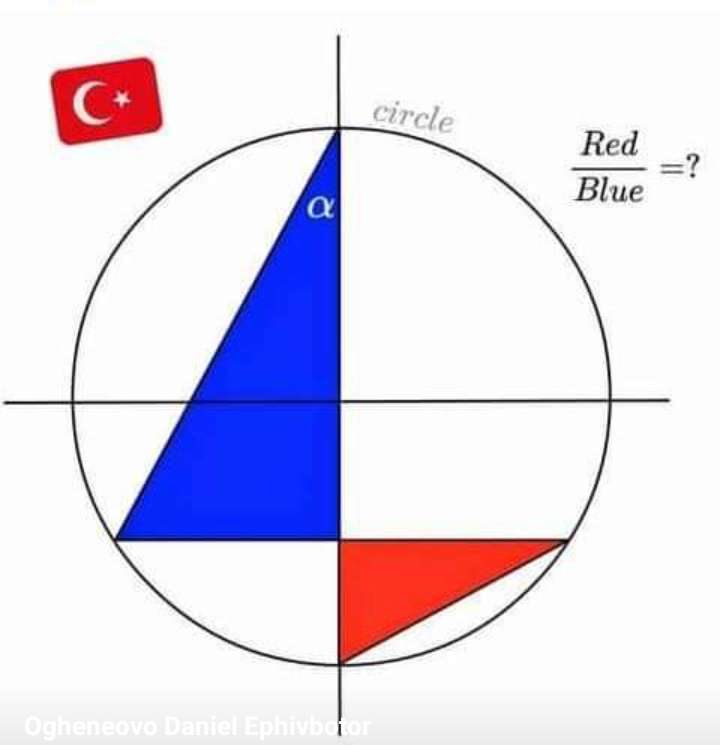
Area red/Area Blue = ⅓
Please, move the above question left/right one time to review the solution of the question.
Thank you kindly.
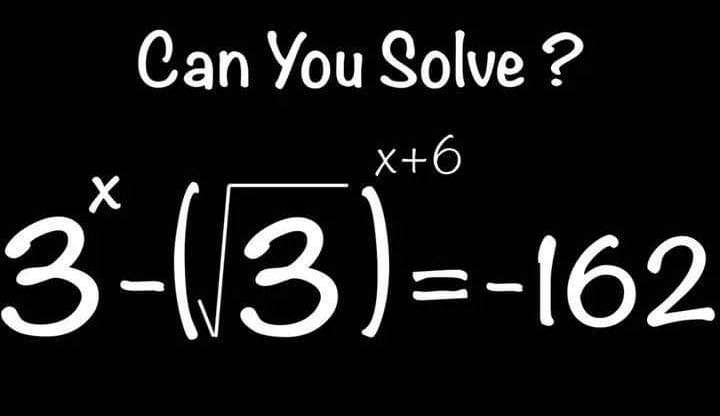
3^(x) - √(3)^(x)*√(3)^(6) = -162
3^(x) - 3^(x/2)*3^(3) = -162
Let p be 3^(x)
p - 27p^(½) + 162 = 0
p-18p^(½)-9p^(½)p+162 = 0
p^(½)(p^(½)-18)-9(p^(½)-18) = 0
(p^(½)-18) = 0 or (p^(...