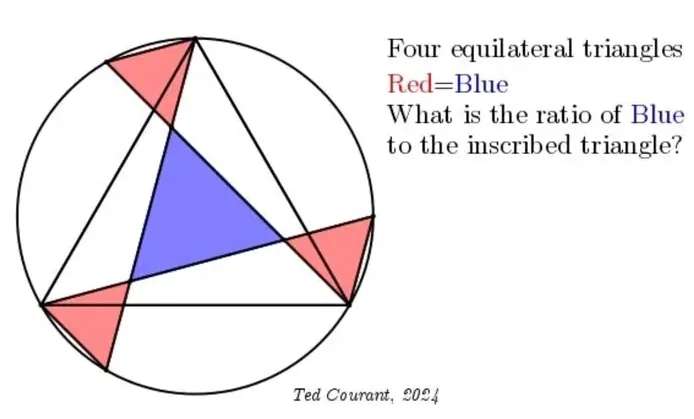
Mathematics Question and Solution
Let the side length of the blue inscribed equilateral triangle be 1 unit.
Area blue equilateral triangle is,
0.5*1²*sin60
= ¼√(3) square units.
= 0.4330127019 square units.
It implies;
⅓(¼√(3)) = ½*a²*sin60
⅙ = ½*a²
a² = ⅓
a = √(⅓)
a = ⅓√(3) units.
a is the side length of each of the three congruent red regular triangles.
Therefore;
b = 2a+1
b = 2*⅓√(3)+1
b = ⅓(2√(3)+3) units.
c² = (⅓(2√(3)+3))²+(⅓√(3))²-2*⅓√(3)*⅓(2√(3)+3)cos120
c² = ⅑(12+12√(3)+9)+⅓+⅑(6+3√(3))
c² = ⅓(4)+⅓(4√(3))+1+⅓+⅓(2)+⅓√(3))
c² = 3+⅓+⅓(5√(3))
c² = ⅓(10)+⅓(5√(3))
c² = ⅓(10+5√(3))
c = √(⅓(10+5√(3))) units.
c = 2.0195765214 units.
c is the side length of the inscribed regular triangle.
Area inscribed regular triangle is;
½*c²*sin60
= ½*⅓(10+5√(3))*½√(3)
= (10√(3)+15)/12 square units.
Therefore;
Area Blue : Area Inscribed Regular Triangle is;
¼√(3) : (10√(3)+15)/12
= √(3) : ⅓(10√(3)+15)
= 3√(3) : (10√(3)+15)
= (90-45√(3))/(300-225)
= (90-45√(3))/75
= ⅗(2-√(3))
= 0.1607695155