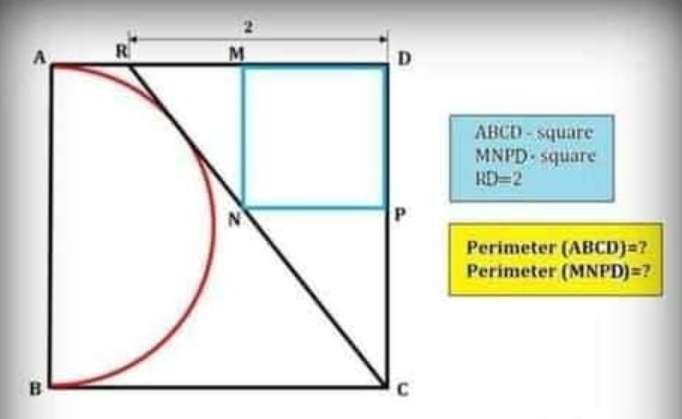
Mathematics Question and Solution
Let MN=NP=PD=MD=y.
Let AR=x.
Therefore;
AD=AB=BC=CD=2+x.
RD=2.
RM=2-y.
And;
RC=2+2x.
There deriving an equation.
Considering similar triangle RCD and RNM.
It implies;
2-y=2
y =2+x, cross multiply.
2y=(2-y)(2+x)
2y=4+2x-2y-xy
4y+xy=4+2x
y(4+x)=4+2x
Therefore;
y=(4+2x)/(4+x)--- (1)
Calculating x, considering triangle RCD, applying Pythagoras rule.
Therefore;
(2+2x)²=2²+(2+x)²
4+8x+4x²=4+4+4x+x²
3x²+4x-4=0
3x²+6x-2x-4=0
3x(x+2)-2(x+2)=0
(3x-2)(x+2)=0
Therefore;
x≠-2
x=⅔ units.
Calculating y, using (1).
y=(4+2x)/(4+x), and x=⅔
y=(4+2(⅔))/(4+⅔)
y=(16/3)÷(14/3)
y=(16/14)
y=(8/7) units.
Perimeter (P1) ABCD will be;
P1=4(AD)
And AD=⅔+2=8/3
P1=4(8/3)
P1=⅓(32) units.
Perimeter (P2) MNPD will be;
P2=4(MN)
And MN=y=8/7
P2=4(8/7)
P2=(32/7) units.