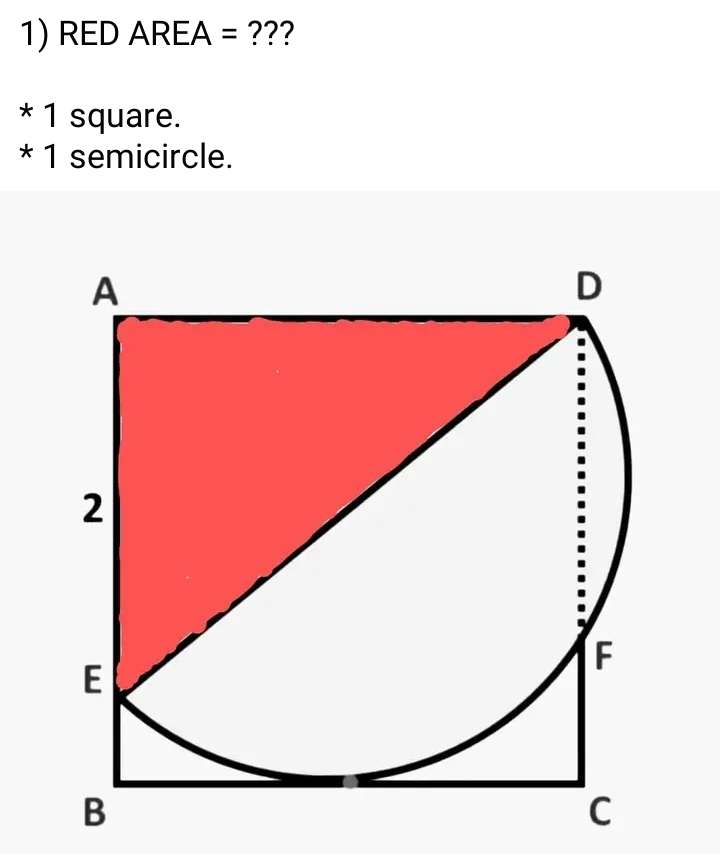
a = (2+x) units.
a is an adjacent of the inscribed red triangle.
b = (2+2x) units.
b is the diameter of the half circle.
2²+(2+x)² = (2+2x)²
4+4+4x+x² = 4+8x+4x²
8+4x+x² = 4+8x+4x²
3x²+4...
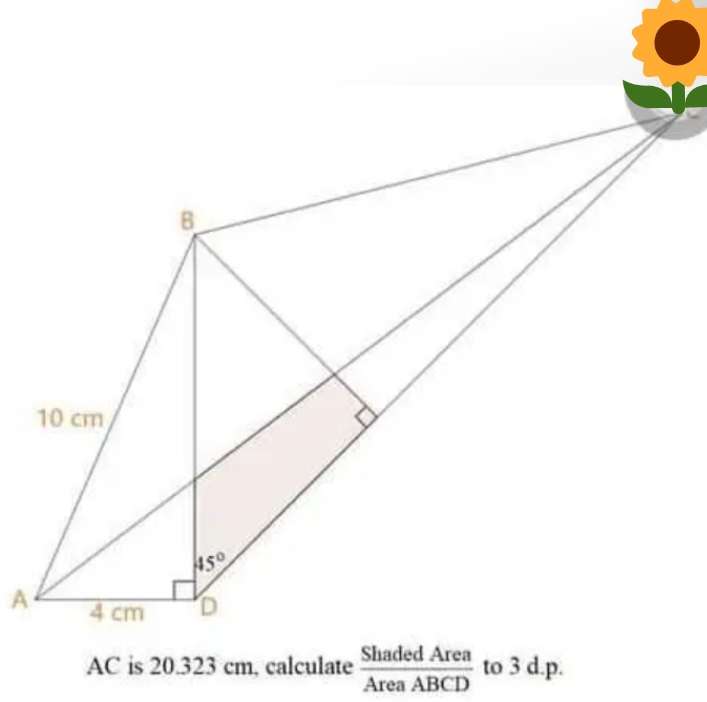
Shaded area is;
Area triangle with height = base = √(42) cm - area triangle with height 6.15093874956 cm and base 4.39211425448, and angle 53°
= ½(√(42))² - ½(6.15093874956*4.39211425448)sin5...
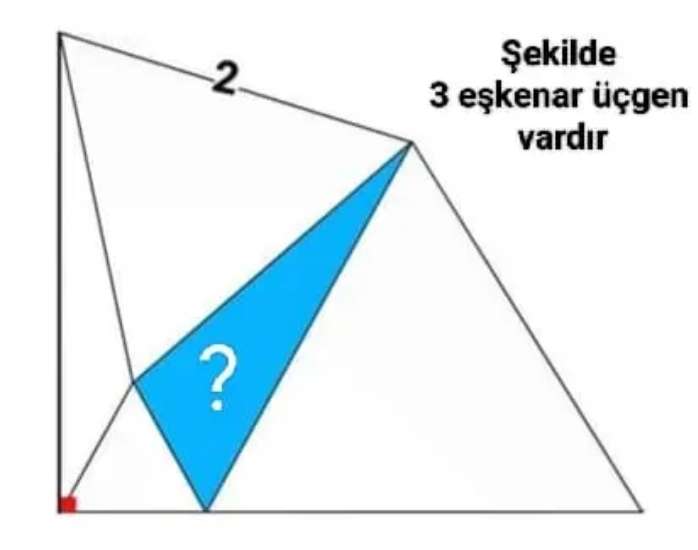
Let the side length of the big inscribed regular triangle be a.
It implies, the side length of the biggest inscribed regular triangle is 3a.
Calculating a.
2² = a²+(2a)²-2*a*2acos120
4 =...
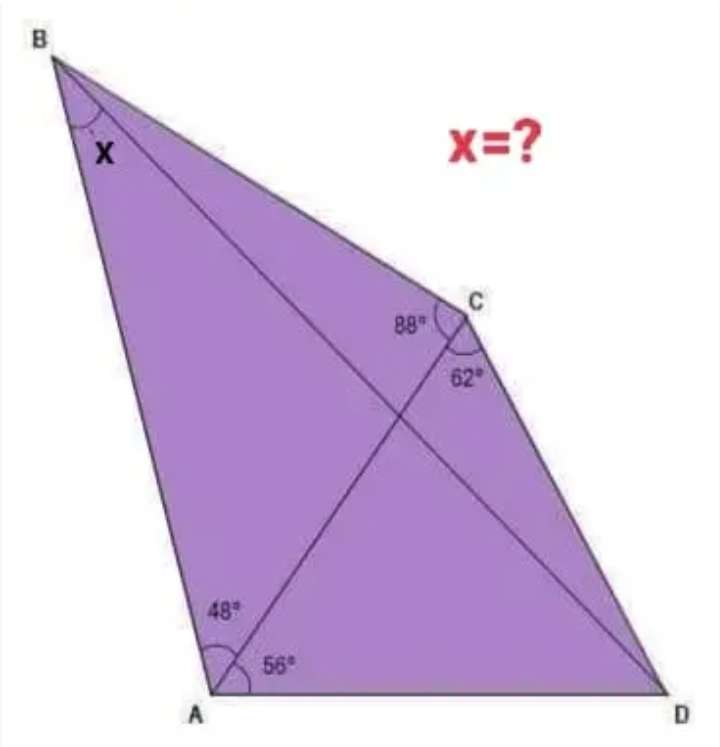
Let AD = 1 unit.
a = 180-62-56
a = 62°
a is angle ADC.
It implies;
AD = AC = 1 unit.
b = 180-48-88
b = 44°
b is angle ABC.
(1/sin44) = (c/sin88)
c = 1.4386796007 units.
c is AB...
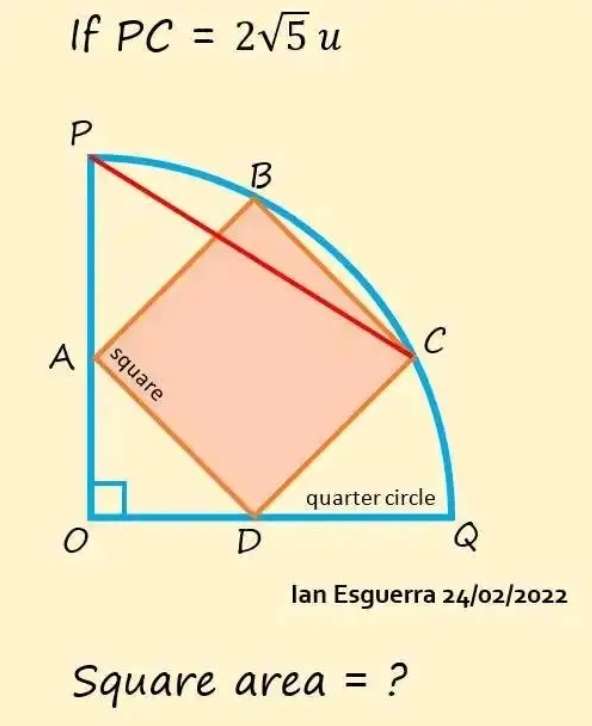
Let the inscribed square side length be a.
b² = 2a²
b = √(2)a units.
b is AC = BD, the diagonal of the inscribed square.
a² = 2c²
Where c is OA = OD.
c² = ½(a²)
c = √(a²/2)
c = ½(√(2)a)...
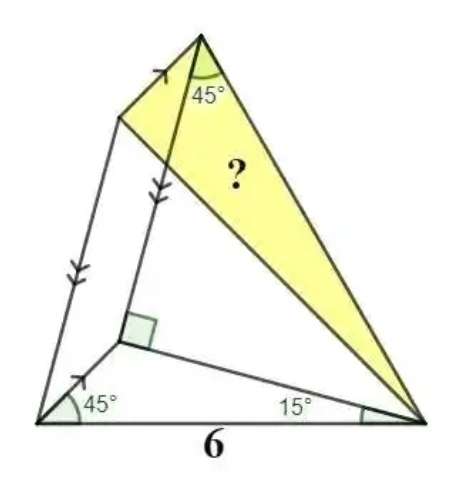
a = 180-45-15
a = 120°
b = 360-120-90
b = 150°
c = ½(360-2(150))
c = ½(60)
c = 30°
d = 30+45
d = 75°
e = 150-90
e = 60°
(6/sin60) = (f/sin75)
f = 6.6921304299 units.
(6/sin...
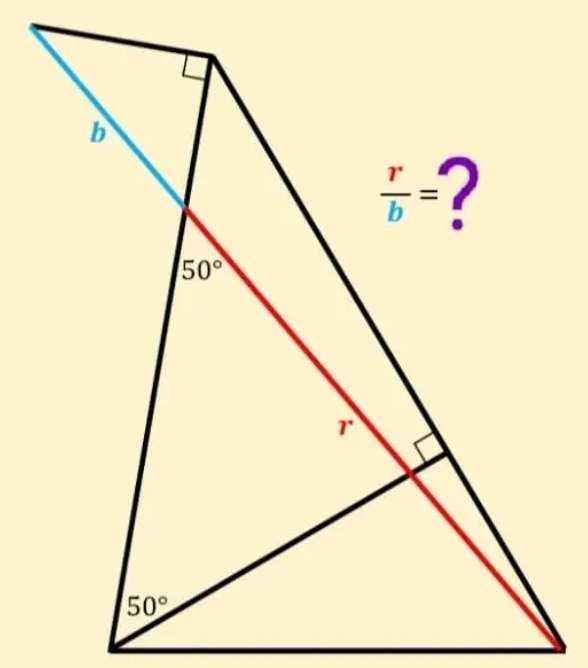
Let b = 2 units.
sin50 = c/2
c = 1.5320888862 units.
cos50 = d/2
d = 1.2855752194 units.
e = 180-50
e = 130°
f = 180-130-40
f = 10°
Calculating r.
(1.2855752194/sin10) = (r/si...
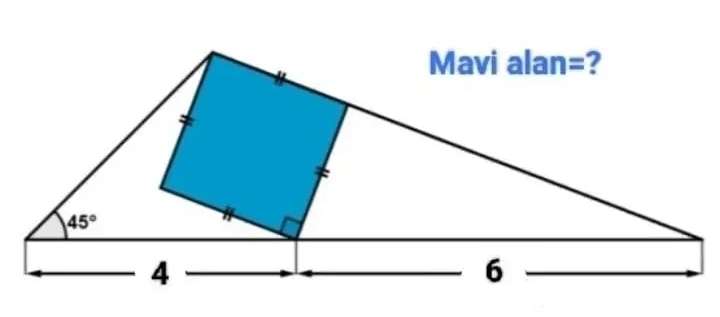
Let the side length of the inscribed blue square be a.
b²+a² = 6²
b = √(36-a²) units.
c = a+b
c = (a+√(36-a²)) units.
It implies;
(a+√(36-a²)) - 6
10 - (a+√(36-a²))
Cross Multiply...
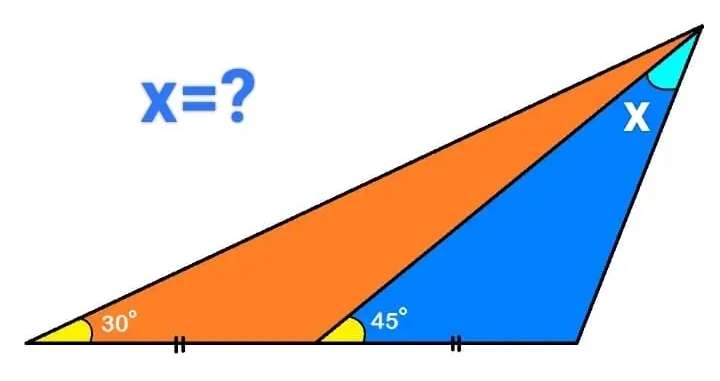
Let the base of the triangle be 2 units.
a = 180-30-135
a = 15°
(1/sin15) = (b/sin135)
b = 2.7320508076 units.
c² = 2²+2.7320508076²-2*2*2.7320508076cos30
c = 1.4142135624 units.
There...
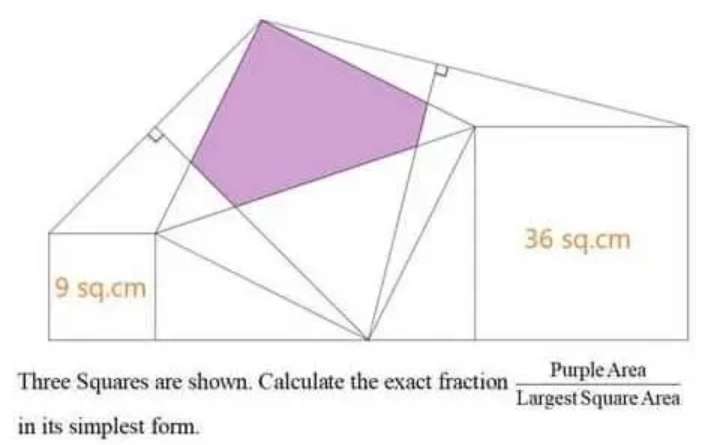
Sir Mike Ambrose is the author of the question.
Area largest square is;
(3√(5))²
= 45 cm²
Area purple is;
Area triangle with height equal base equal 3√(5) cm - area triangle with side 2....