
a² = 24²+7²
a = √(625)
a = 25 units.
b = 7+a
b = 32 units.
c² = 32²+24²
c = √(1600)
c = 40 units.
d = ½(c)
d = 20 units.
It implies, the required length, x is;
25² = x²+20²
x²...
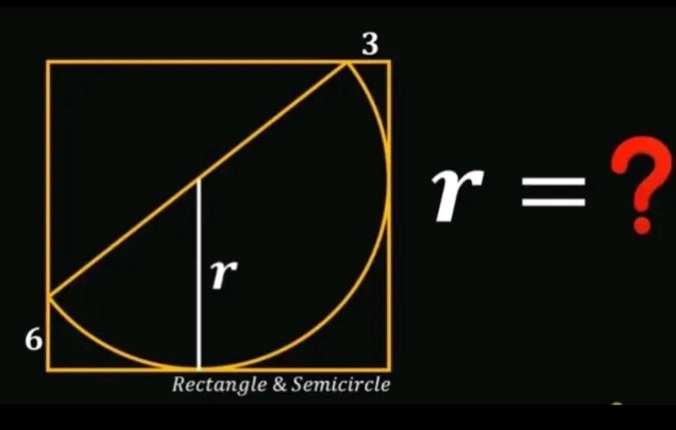
Calculating r, radius of the inscribed half circle.
a = (r-6) units.
b = (r-3) units.
Therefore;
r² = a²+b²
r² = (r-6)²+(r-3)²
r² = r²-12r+36+r²-6r+9
r²-18r+45 = 0
Resolving the a...
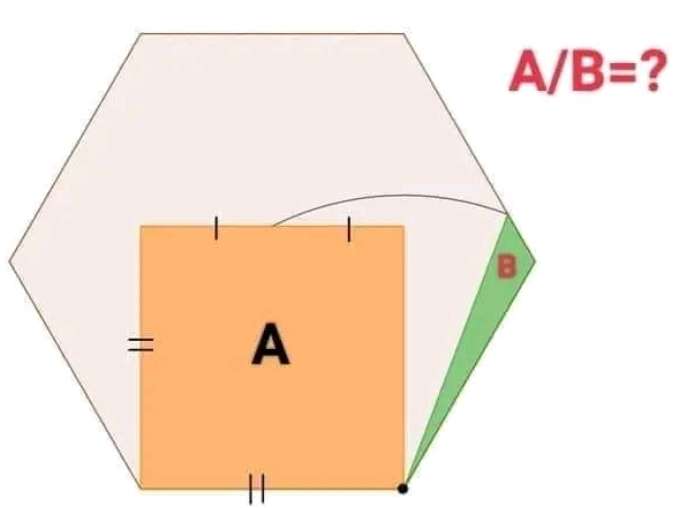
Let the side length of the regular hexagon be 1 unit.
Therefore, area A (area inscribed square) is;
1²
= 1 square unit.
Calculating area B.
a² = 1²+(½)²
a² = 1+¼
a = √(5/4)
a = ½√(5...
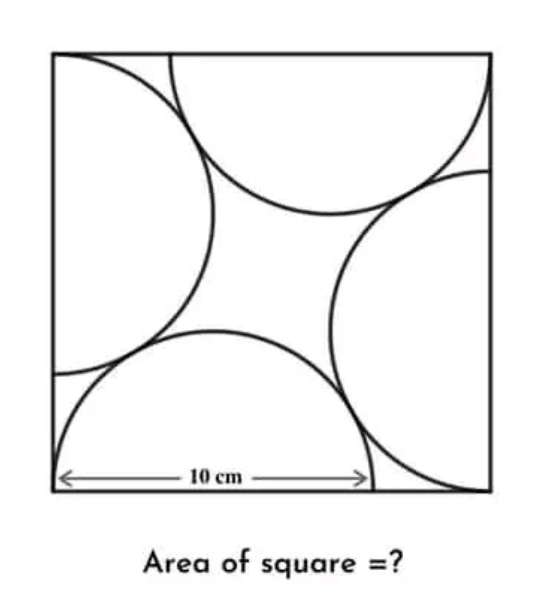
Let the single side length of the square be (x+10) unit.
Calculating x.
10²=(5+x)²+5²
100-25-25=10x+x²
Therefore;
x²+10x-50=0
Resolving the above quadratic equation via completing the squ...
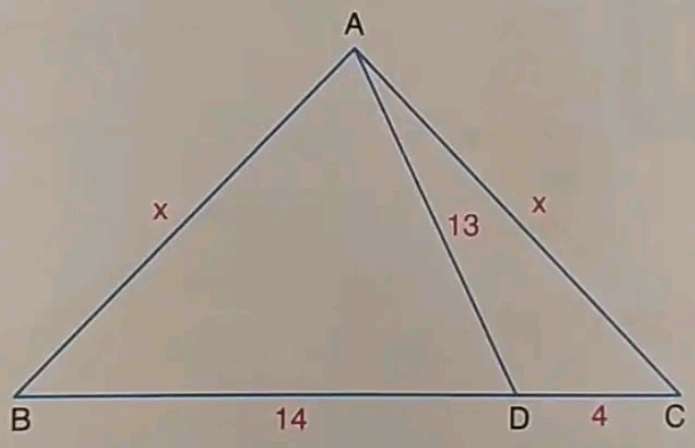
Calculating x, length AC = length AB.
a = 14+4
a = 18 units.
b = ½(18)
b = 9 units.
c²+9² = x²
c = √(x²-81) units.
d = 9-4
d = 5 units.
It implies;
13² = √(x²-81)²+5²
169 =...
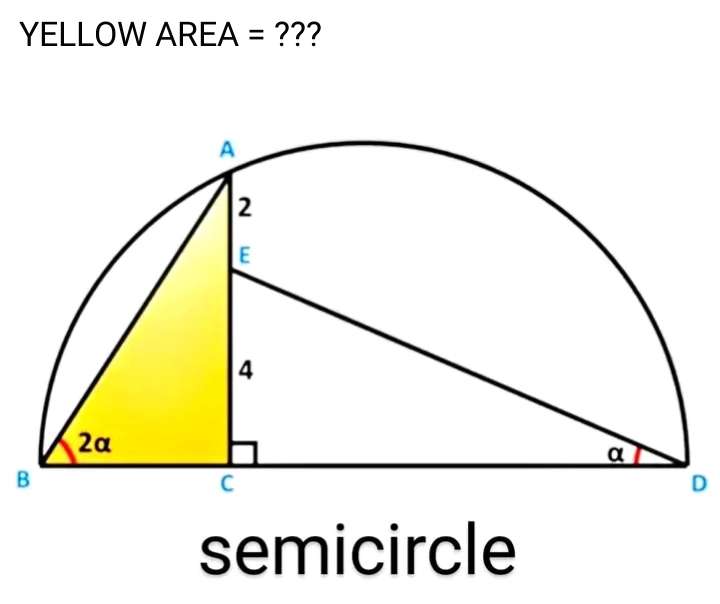
Let CD be b units.
Let BC be a units.
c = 2+4
c = 6 units.
Observing similar plane shape (right-angled) side length ratios.
a - 6
6 - b
Cross Multiply.
ab = 36 --- (1).
Let alph...
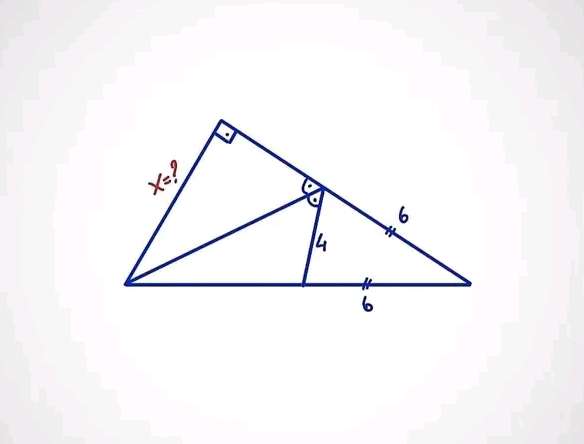
tana = (0.5*4)/6
tana = ⅓
a = atan(⅓)°
b = 2a
b = 2atan(⅓)°
c = ½(180-b)
c = ½(180-36.8698976458)
c = 71.5650511771°
d = c+½(180-c)
d = 125.7825255886°
e = 180-d
e = 54.2174744115°
f = 180-125....
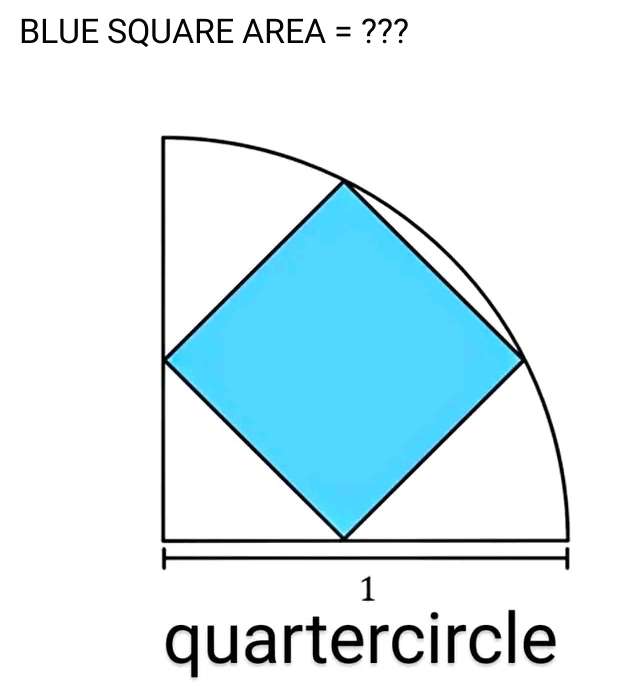
Let a be the side length of the inscribed blue square.
b² = 2a²
b = √(2)a units.
2c² = a²
c = √(a²/2)
c = ½√(2)a unit.
It implies;
1² = (√(2)a)²+(½√(2)a)²
1 = 2a²+½(a²)
1 = ½(5a²)...
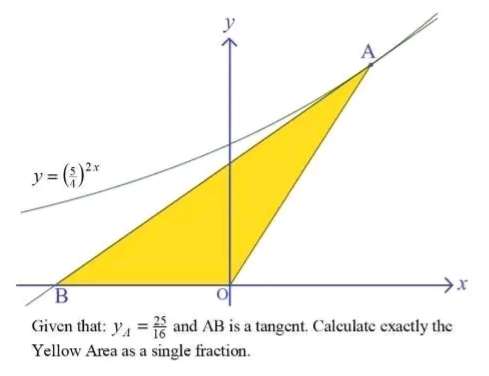
For y = (25/16) unit.
x is;
(25/16) = (5/4)^(2x)
2x = 2
x = 1 unit.
Gradient of the curve at x equal 1 unit is;
dy/dx = (25/8)ln(5/4)
At y = 0 at the tangent, x is;
x = (50ln(5/4)-25)/50ln(5/4)...
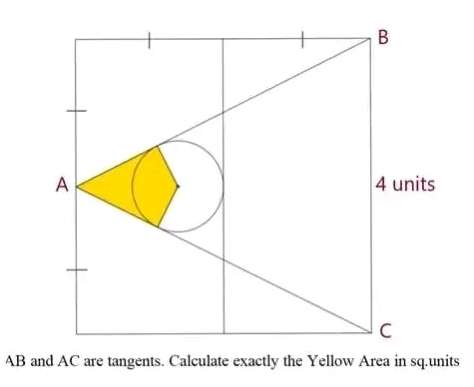
Radius of the inscribed circle, r is;
√(5)r + r = 2
r = 2/(√(5)+1) unit.
r = ½(√(5)-1) unit
Therefore;
Area Yellow exactly is square units is;
2(area triangle with height (√(5)-1) unit...