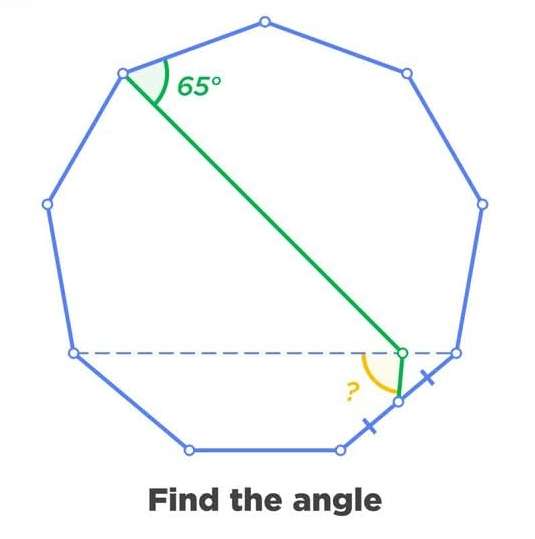
Mathematics Question and Solution
Calculating the required angle.
Let it be x.
a = ⅑*180(9-2)
a = 20*7
a = 140°
a is the single interior angle of the regular nonagon.
b = ½(140)-65
b = 5°
c = ½(180(5-2)-3(140))
c = ½(540-420)
c = ½(120)
c = 60°
d = 140-c
d = 80°
e = ½(140)-c
e = 70-60
e = 10°
Let the side length of the regular nonagon be 2 units.
f² = 2(2)²-2(2)²cos140
f = 3.75877048314 units.
g = 70-½(180-140)+5
g = 70-20+5
g = 55°
f = 140-20-½(360-2(140))
f = 140-20-40
f = 80°
g = 180-55-80
g = 45°
(h/sin80) = (3.75877048314/sin45)
h = 5.23494670406 units.
tan80 = j/1
j = 5.67128181962 units.
k² = 5.67128181962²+5.23494670406²-2*5.67128181962*5.23494670406cos5
k = 0.64524295393 units.
(0.64524295393/sin5) = (5.67128181962/sinl)
l = 50°
m = 180-l
m = 180-50
m = 130°
Therefore, the required angle x is;
x = m-g
x = 130-45
x = 85°