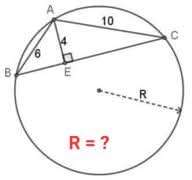
Mathematics Question and Solution
Calculating R, radius of the circle.
a²+4² = 6²
a = √(36-16)
a = √(20)
a = 2√(5) units.
b²+4² = 10²
b = √(100-16)
b = √(84)
b = 2√(21) units.
Therefore;
2√(5)*2√(21) = 4c
c = √(105) units.
d = 4+c
d = (4+√(105)) units.
d = 14.246950766 units.
e = ½(d)
e = 7.123475383 units.
f = ½(a+b)
f = ½(2√(5)+2√(21))
f = (√(5)+√(21)) units.
g = f-a
g = (√(5)+√(21))-2√(5)
g = (√(21)-√(5)) units.
g = 2.34650771746 units.
Therefore R, radius of the circle is;
R² = e²+g²
R² = 7.123475383²+2.34650771746²
R = √(56.2500000003)
R = 7.5 units.
Or
cosa = 4/6
a = acos(⅔)°
cosb = 4/10
b = acos(2/5)°
c = 180-a-b
c = 180-acos(⅔)-acos(2/5)
c = 65.388493374°
d = √(6²-4²)+√(10²-4²)
d = √(20)+√(84)
d = 13.6372873449 units.
e = ½(d)
e = 6.81864367246 units.
Therefore R, radius of the circle is;
sinc = e/R
sin65.388493374 = 6.81864367246/R
R = 6.81864367246/sin(65.388493374)
R = 7.5 units.