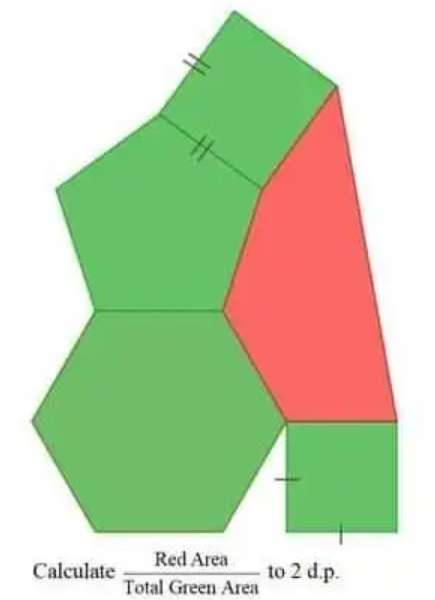
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the side length of the regular hexagon be 1 unit.
Therefore;
Area green is;
Area regular hexagon with side 1 unit + Area regular pentagon with side 1 unit + Area square with side 1 unit + Area square with side ½√(3) units.
= (6/4tan(180/6)) + (5/4tan(180/5)) + 1² + (½√(3))²
= 2.59807621135 + 1.72047740059 + 1 + (3/4)
= 6.06855361194 space units.
Area red is;
Area triangle with two side 1 unit and ½√(3) units, and angle 120° + Area triangle with two side 1 unit and 1.61741318276 units, and angle 104.37365913° + Area triangle with two side 1 unit and 2.10215448576 units, and angle 113.813156806°
= 0.5*½√(3)sin120 + 0.5*1.61741318276sin104.37365913 + 0.5*2.10215448576sin113.813156806
= 0.375 + 0.7833919645 + 0.96159586062
= 2.11998782512 space units.
It implies;
Area Red ÷ Area Green Total to 2 d. p. is;
2.11998782512 ÷ 6.06855361194
= 0.34933988569
≈ 0.35