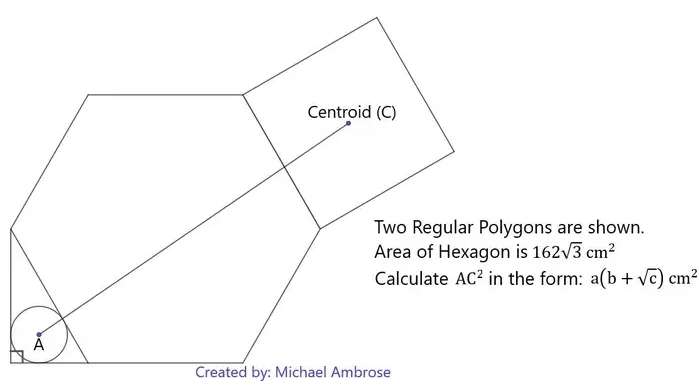
Mathematics Question and Solution
Let a be the side length of the regular hexagon.
sin30 = b/a
b = ½(a) cm.
c = 2b+a
c = 2a cm.
cos30 = d/a
d = ½√(3)a cm.
e = ½(162√(3)) cm²
e = 81√(3) cm²
e is half the area of the regular hexagon.
Calculating a.
½(2a+a)*½√(3)a = 81√(3)
¼(3a²) = 81
a² = 27*4
a = 6√(3) cm.
Again, a is the side length of the regular hexagon.
sin30 = f/(6√(3))
f = 3√(3) cm.
Let g be the radius of the inscribed circle.
h = (3√(3)-g) cm.
tan30 = g/(3√(3)-g)
√(3)g = (3√(3)-g)
g(√(3)+1) = 3√(3)
g = ½(9-3√(3)) cm.
g = 1.9019237886 cm.
Again, g is the radius of the inscribed circle.
Recall.
h = 3√(3)-g
h = 3√(3)-½(9-3√(3))
h = ½(6√(3)-9+3√(3))
h = ½(9√(3)-9) cm.
cos30 = ½(9-3√(3))/j
√(3)j = 9-3√(3)
j = ⅓(9√(3)-9)
j = (3√(3)-3) cm.
k = a-j
k = 6√(3)-3√(3)+3
k = (3√(3)+3) cm
tan30 = l/(½(9-3√(3)))
l = (9-3√(3))/(2√(3))
l =½(3√(3)-3) cm.
m = h+a+l
m = ½(9√(3)-9)+6√(3)+½(3√(3)-3)
m = ½(9√(3)-9+12√(3)+3√(3)-3)
m = ½(24√(3)-12)
m = (12√(3)-6) cm.
n² = (12√(3)-6)²+(3√(3)+3)²-2(3√(3)+3)*(12√(3)-6)cos120
n = 20.1727170402 cm.
(20.1727170402/sin120) = ((12√(3)-6)/sino)
o = 39.3985611553°
p = 120-o
p = 80.6014388447°
q² = 2a²
q² = 2(6√(3))²
q² = 216
q = √(216)
q = 6√(6) cm.
q = 14.6969384567 cm.
r = ½(q)
r = 3√(6) cm.
r = 7.3484692283 cm.
s = 45+p
s = 125.6014388447°
Therefore, (AC)² exactly in decimal cm² is;
(AC)² = 7.3484692283²+20.1727170402²-2*7.3484692283*20.1727170402cos125.6014388447
AC = 25.1700366231 cm.
It implies;
(AC)² = 633.5307436082 cm²