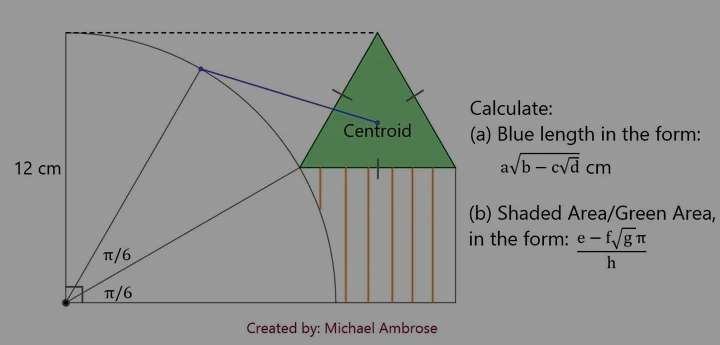
Mathematics Question and Solution
sin30 = a/12
a = 6 cm.
Where a is the height of the green regular triangle.
sin60 = 6/b
½√(3) = 6/b
b = 12/√(3)
b = 4√(3) cm.
b is the side length of the green regular triangle.
tan30 = c/(0.5*4√(3))
1/√(3) = c/2√(3)
c = 2 cm.
cos60 = d/12
d = 6 cm.
sin60 = e/12
e = 6√(3) cm.
cos30 = f/12
f = 6√(3) cm.
g = f-d+½(b)
g = 6√(3)-6+2√(3)
g = (8√(3)-6) cm.
h = e-d-c
h = (6√(3)-8) cm.
Therefore, blue length is;
Let it be j.
j² = (8√(3)-6)²+(6√(3)-8)²
j² = 400-192√(3)
j² = 16(25-12√(3))
j = 4√(25-12√(3)) cm.
Again, j is the required blue length.
Calculating Shaded Area/Green Area.
Green Area is;
½*4√(3)*4√(3)sin60
= 12√(3) cm²
Shaded Area is;
(½*(4√(3)+4√(3)+6√(3))*6) - (30π*12*12/360)
= 3(14√(3))-12π
= (42√(3)-12π) cm²
It implies;
Shaded Area ÷ Area Green is;
(42√(3)-12π)÷(12√(3))
= (7√(3)-2π)÷(2√(3))
= (21-2√(3)π)/6 cm²