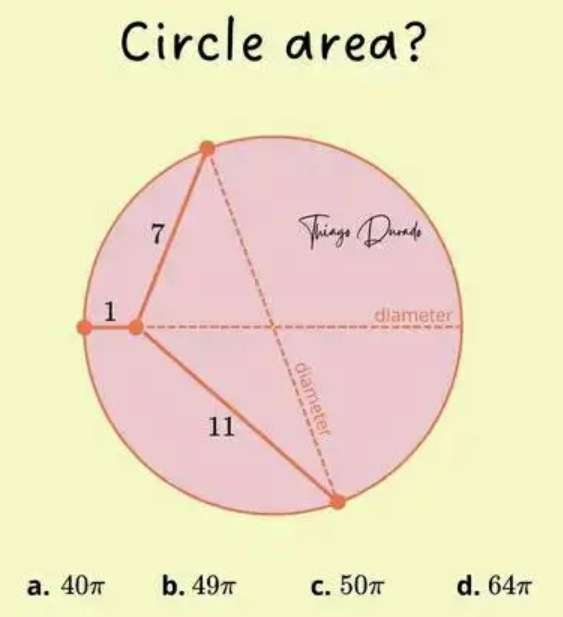
Mathematics Question and Solution
Let a be the radius of the circle.
b = (a-1) units.
7² = a²+b²-2abcosc --- (1).
11² = a²+b²+2abcosc --- (2).
At (1).
7² = a²+b²-2abcosc
2abcosc = a²+b²-49 --- (3).
Substituting (3) in (2).
11² = a²+b²+a²+b²-49
121 = 2a²+2b²-49
2a²+2b² = 170
a²+b² = 85 --- (4).
And b = a-1
Therefore;
a²+(a-1)² = 85
a²+a²-2a+1 = 85
2a²-2a-84 = 0
a²-a-42 = 0
a²-7a+6a-42 = 0
a(a-7)+6(a-7) = 0
(a+6)(a-7) = 0
It implies;
a ≠ -6
a = 7 units.
Again, a is the radius of the circle.
Area Circle is;
πa²
= π(7²)
= 49π square units.