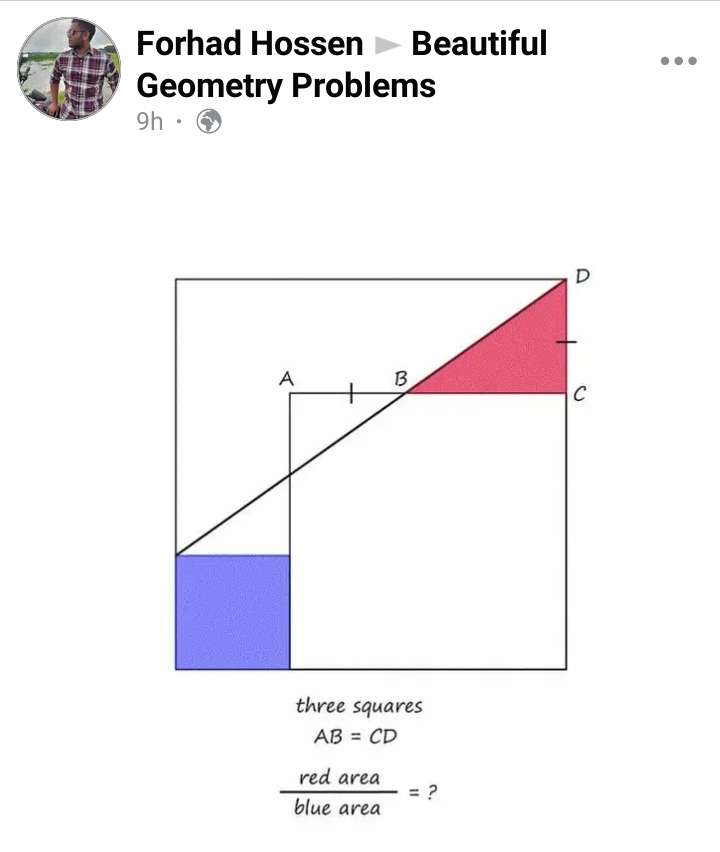
Mathematics Question and Solution
Let AB = CD = 2 units.
Let the big inscribed square side length be a.
Considering similar triangle ratios, calculating a.
(a-2) = (2+a)
2 = a
Cross Multiply.
a²-2a = 4+2a
a²-4a-4 = 0
(a-2)² = 4+4
a = 2±2√(2)
a ≠ 2-2√(2) units.
a = 2+2√(2) units.
Again, a is the big inscribed square side length.
BC = a-AB
BC = 2+2√(2)-2
BC = 2√(2) units.
Notice;
Area Blue is;
2²
= 4 square units.
Area red is;
½*2*2√(2)
= 2√(2) units.
It implies;
Area Red ÷ Area Blue is;
2√(2)÷4
= ½√(2)