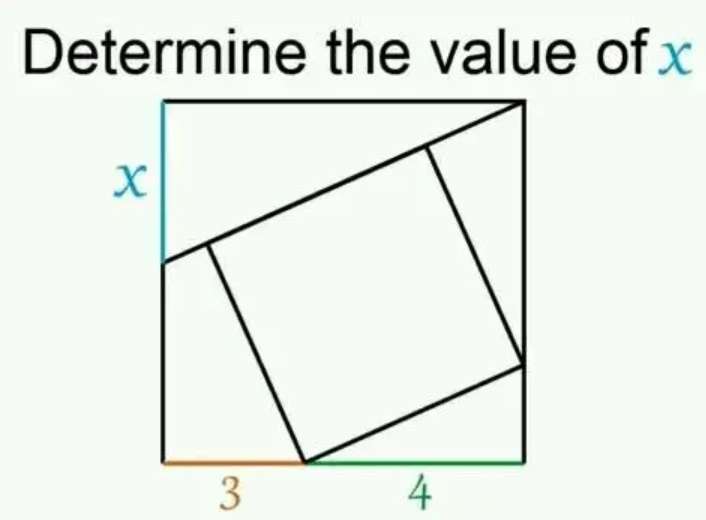
Mathematics Question and Solution
Calculating length x.
a = 4+3
a = 7 units.
a is the side length of a ascribed square.
b² = 2*7²
b = 7√(2) units.
b is the diagonal of the ascribed square.
Let the side length of the inscribed square be y.
y² = 4²+c²
c² = y²-16
c = √(y²-16) units.
4 - y
y - d
Cross Multiply.
d = ¼(y²) units.
It implies;
c+d = a
√(y²-16)+¼(y²) = 7
4√(y²-16)+y² = 28
16y²-256 = (28-y²)²
16y²-256 = 784-56y²+y⁴
y⁴-72y²+1040 = 0
Let y² = p
It implies;
p²-72p+1040 = 0
(p-36)² = -1040+(-36)²
(p-36)² = 256
p = 36±√(256)
p = 36±16
p ≠36+16
p = 36-16
p = 20 units.
And p = y²
y = √(p)
y = √(20)
y = 2√(5) units.
y = 4.472135955 units.
Again, y is the side length of the inscribed square.
Recall.
c = √(y²-16)
And y = 2√(5) units.
c = √((2√(5))²-16)
c = √(20-16)
c = 2 units.
e = a-c
e = 7-2
e = 5 units.
sinf = 2√(5)/5
f = asin(2√(5)/5)°
g = 90-f
g = (90-asin(2√(5)/5))°
Therefore, the required length, x is;
tang = x/a
tan(90-asin(2√(5)/5)) = x/7
x = 7tan(90-asin(2√(5)/5))
x = ½(7)
x = 3.5 units.