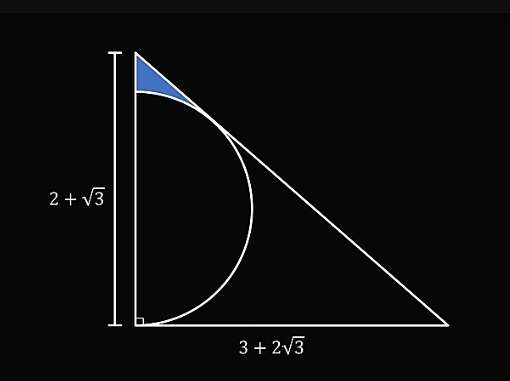
Mathematics Question and Solution
Calculating area shaded blue.
a² = (2+√(3))²+(3+2√(3))²
a² = 4+4√(3)+3+9+12√(3)+12
a² = 28+16√(3)
a = √(28+16√(3)) units.
a = 7.4641016151 units.
a is the hypotenuse of the ascribed right-angled triangle.
Let b be the radius of the inscribed half circle.
c = (2+√(3))-b
c = (3.7320508076-b) units.
d = √(28+16√(3))-(3+2√(3))
d = 7.4641016151-6.4641016151
d = 1 unit.
Calculating b.
(3.7320508076-b)² = 1²+b²
13.9282032303-7.4641016151b = 1
12.9282032303 = 7.4641016151b
b = 1.7320508076 units.
b = √(3) units.
b is the radius of the inscribed half circle.
tane = 1/√(3)
e = 30°
Therefore, area shaded blue is;
Area triangle with height 1 unit and base √(3) units - Area sector with radius √(3) units.
= (½*√(3)*1)-(30π*√(3)²/360)
= ½√(3)-¼(π)
= ¼(2√(3)-π) square units.
= 0.0806272404 square units.