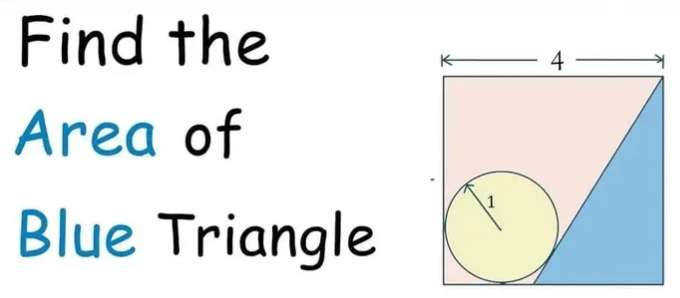
Mathematics Question and Solution
Let a be the base of the blue inscribed triangle.
b = 4-1-a
b = (3-a) units.
c² = 2(1)²
c = √(2) units.
d² = 2(4)²
d = 4√(2) units.
e = d-c
e = 3√(2) units.
f² = a²+4²
f = √(a²+16) units.
g²+1² = (3√(2))²
g² = 18-1
g = √(17) units.
h = g+b
h = (√(17)+(3-a)) units.
Therefore, equating f and h to get a, the base of the blue inscribed triangle.
√(a²+16) = (√(17)+(3-a))
a²+16 = (√(17)+(3-a))²
a²+16 = ((√(17)+3)-a)²
a²+16 = (7.1231056256-a)²
16 = 50.7386337537-14.2462112512a
14.2462112512a = 34.7386337537
a = 2.4384471872 units.
Again, a is the base of the inscribed blue triangle.
Area triangle blue is;
½(4a)
= 2*2.4384471872
= 4.8768943744 square units.