Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
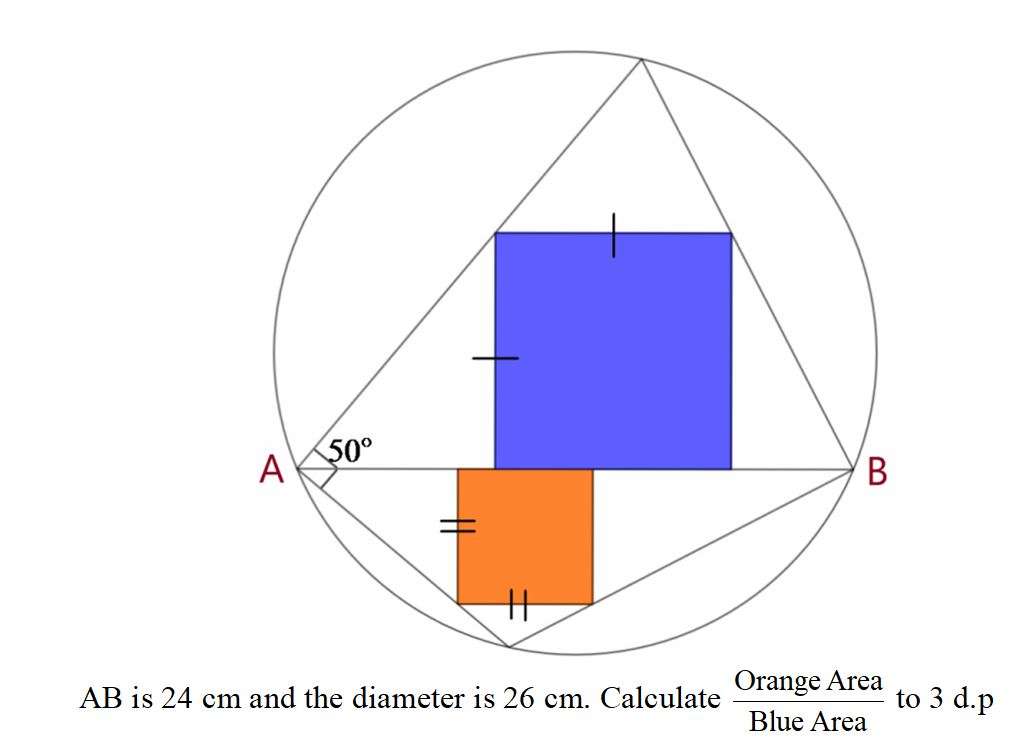
Radius of the ascribed circle is 13 cm.
a = acos((2*13²-24²)/(2*13²))
a = 134.76027010392°
b = ½(a)
b = 67.38013505196°
c = 40°
d = b - c
d = 27.38013505196°
e = 90 - d
e = 62.61986494804°
Let the side of the inscribed blue square be f.
Calculating f.
(f/tan50)+f+(f/tan62.61986494804) = 24
f = 24/((1/tan50)+1+(1/tan62.6198644804))
f = 10.18238945915 cm.
Area Blue is;
f²
= (10.18238945915)²
= 103.68105509785 cm²
g = ½(360 - 134.76027010392)
g = 112.61986494804°
h = 180-40-g
h = 27.38013505196°
Let the side of the inscribed orange square be i.
Calculating i.
(i/tan40)+i+(i/tan27.38013505196) = 24
i = 24/((1/tan40)+1+(1/tan27.38013505196))
i = 5.82158678444 cm
Area Orange is;
i²
= (5.82158678444)²
= 33.89087268882 cm²
Therefore;
Area Orange ÷ Area Blue to 3 decimal places is;
33.89087268882 ÷ 103.68105509785
= 0.32687623266
≈ 0.327