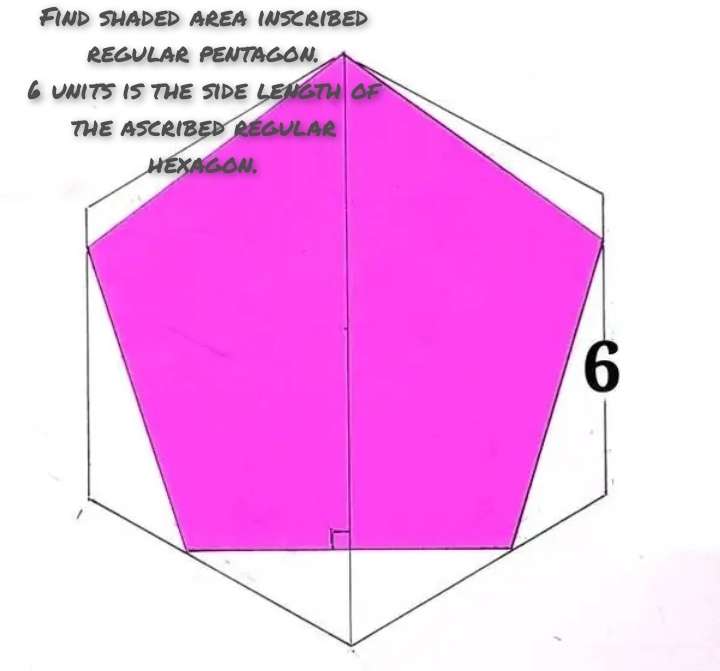
Mathematics Question and Solution
sin30 = a/6
a = 3 units.
b = 6+2a
b = 12 units.
Let the side length of the inscribed regular pentagon be c.
Calculating c.
d² = 2c²-2c²cos108
108° is the single interior angle of the regular pentagon.
d = 1.6180339887c units.
e²+(0.5c)² = (1.6180339887c)²
e = 1.5388417685c units.
tan60 = 0.5c/f
f = 0.2886751346c units.
It implies;
e+f = b
1.5388417685c+0.2886751346c = 12
1.8275169031c = 12
c = 6.5662867357 units.
Again, c is the side length of the inscribed regular pentagon.
Therefore;
d = 1.6180339887c
And c = 6.5662867357 units
d = 1.6180339887*6.5662867357
d = 10.6244751179 units.
Area inscribed regular pentagon is;
2(area triangle with height 6.5662867357 units and base 6.5662867357sin108 units) + Area triangle with height 6.5662867357 units and base 10.6244751179sin72 units.
= 2(0.5*6.5662867357*6.5662867357sin108)+0.5*6.5662867357*10.6244751179sin72
= 74.1803126329 square units.
= 74.18 square units to 2 decimal places.