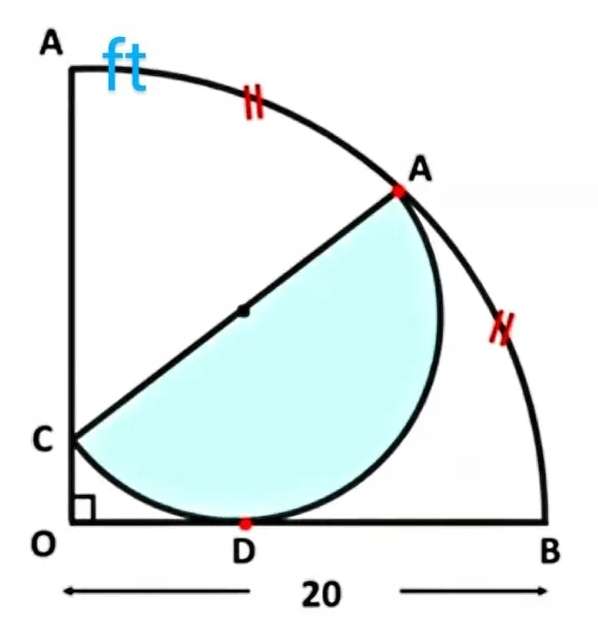
Mathematics Question and Solution
Calculating blue inscribed half circle area.
Let the radius of the blue inscribed half circle be a.
20² = 2b²
b² = 200
b = √(200)
b = 10√(2) units.
c²+(0.5b)² = a²
c² = a²-(5√(2))²
c = √(a²-50) units.
d = a-c
d = (a-√(a²-50)) units.
d is OC.
Calculating a.
5√(2) - (a-√(a²-50))
10√(2) - 5√(2)
It implies;
½ = (a-√(a²-50))/(5√(2))
Cross Multiply.
2(a-√(a²-50)) = 5√(2)
2a-2√(a²-50) = 5√(2)
2a-5√(2) = 2√(a²-50)
(2a-5√(2))² = 4(a²-50)
4a²-20√(2)a+50 = 4a²-200
250 = 20√(2)a
a = 25/(2√(2))
a = ¼(25√(2)) units.
a = 8.8388347648 units.
Again, a is the radius of the blue inscribed half circle.
It implies;
Area blue inscribed half circle is;
½(a²)π
= ½*¼(25√(2))*¼(25√(2))π
= (625π/16) square units.
= 122.7184630309 square units.