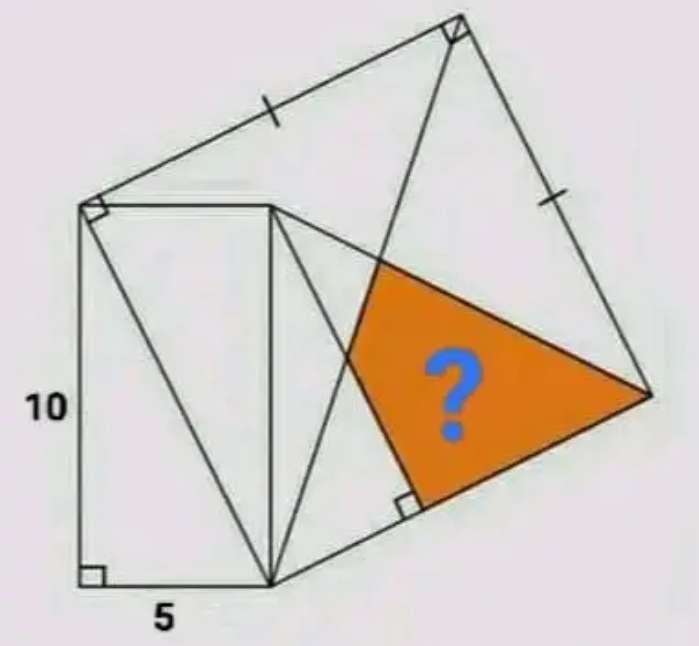
Mathematics Question and Solution
a² = 10²+5²
a = √(125)
a = 5√(5) units.
a is the side length of the square.
b² = 2a²
b² = 2(5√(5))²
b = √(250)
b = 5√(10) units.
b is the diagonal of the square.
c = 90+atan(10/5)
c = (90+atan(2))°
d = 90-atan(5/10)
d = (90-atan(0.5))°
d = atan(2)°
cos(atan(2)) = e/10
e = 4.472135955 units.
f = 5√(5)-e
f = 6.7082039325 units.
2 = g/4.472135955
g = 8.94427191 units.
h = 90-atan(8.94427191/6.7082039325)
h = atan(4/3)°
j = atan(3/4)°
k = 180-45-j
k = 98.1301023542°
It implies;
(5√(5)/sin98.1301023542) = (l/sin45)
l = 7.9859570625 units.
Therefore, the required area (area pink quadrilateral) is;
(0.5(4.472135955+5√(5))*6.7082039325)-(0.5*5√(5)*7.9859570625sin(atan(3/4)))
= 52.5-26.7857142857
= 25.7142857143 square units.
= ⅐(180) square units.