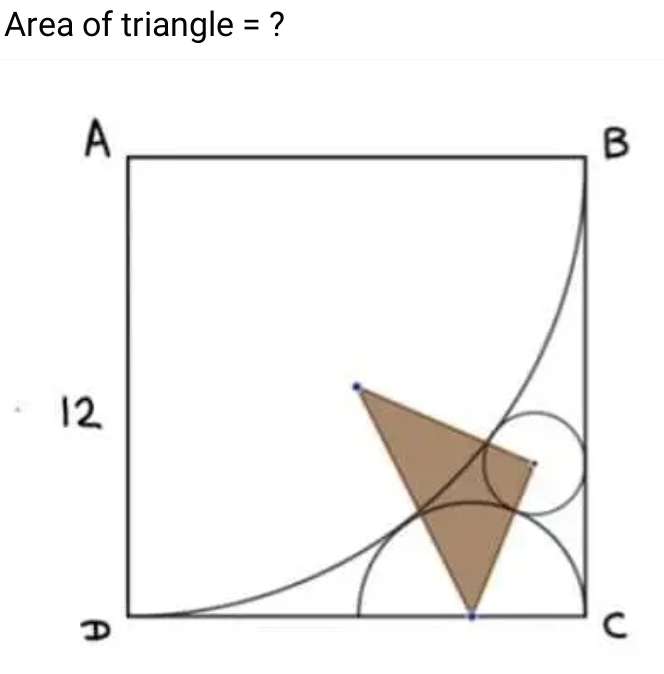
Mathematics Question and Solution
Let a be the radius of the inscribed half circle.
Let b be the radius of the inscribed circle.
c = (12+a) units.
d = (12-a) units.
Calculating a.
(12+a)² = 12²+(12-a)²
48a = 144
3a = 9
a = 3 units.
Again, a is the radius of the inscribed half circle.
e = (3+b) units.
f = (3-b) units.
g² = (3+b)²-(3-b)²
g² = 12b
g = √(12b) units.
h = (12-√(12b)) units.
Calculating b.
(12+b)² = (12-√(12b))²+(12-b)²
48b = 144-24√(12b)+12b
4b = 12-2√(12b)+b
2√(12b) = 12-3b
2²(12b) = (12-3b)²
48b = 144-72b+9b²
9b²-120b+144 = 0
3b²-40b+48 = 0
(b-⅓(20))² = -16+(-⅓(20))²
(b-⅓(20))² = ⅑(-144+400)
(b-⅓(20))² = ⅑(256)
b = ⅓(20)±√(⅑(256))
b = ⅓(20)±⅓(16)
b = ⅓(20±16)
It implies;
b = ⅓(4) units.
Again, b is the radius of the inscribed circle.
j² = 6²+3²
j² = 45
j = 3√(5) units
tank = 6/3
k = atan(2)°
Recall.
e = (3+b)
And b = 4/3 units.
e = 3+(4/3)
e = (13/3) unit.
Recall again.
f = (3-b)
And b = 4/3 units.
f = 3-(4/3)
f = (5/3) units.
cosl = (5/3)/(13/3)
l = acos(5/13)°
m = 180-k-l
m = (180-atan(2)-acos(5/13))°
Therefore, area of the inscribed triangle is;
0.5*3√(5)*(13/3)sin(180-atan(2)-acos(5/13))
= 11 square units.