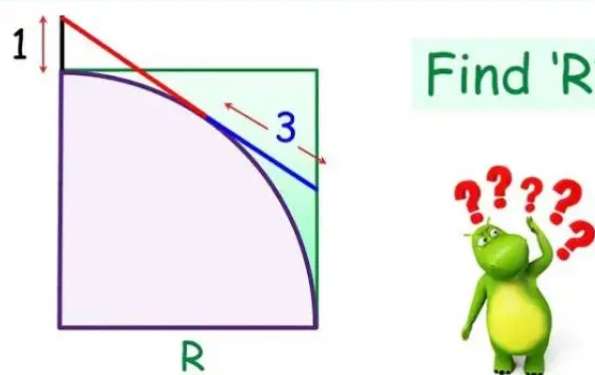
Mathematics Question and Solution
Calculating R, radius of the inscribed quarter circle (side length of the square).
a = (R-3) units.
b = (R+1) units.
Therefore;
(R+1)² = R²+c²
c² = R²+2R+1-R²
c = √(2R+1) units.
d = c+3
d = (3+√(2R+1)) units.
e = a+1
e = (R-3)+1
e = (R-2) units.
R is;
(3+√(2R+1))² = R²+(R-2)²
9+6√(2R+1)+2R+1 = R²+R²-4R+4
6√(2R+1) = 2R²-6R-6
3√(2R+1) = R²-3R-3
18R+9 = R⁴-3R³-3R²-3R³+9R²+9R-3R²+9R+9
18R+9 = R⁴-6R³+3R²+18R+9
0 = R⁴-6R³+3R²
R²-6R+3 = 0
(R-3)² = -3+(-3)²
(R-3)² = 6
R = 3±√(6)
It implies;
R ≠ 3-√(6)
R = (3+√(6)) units.
R = 5.4494897428 units.