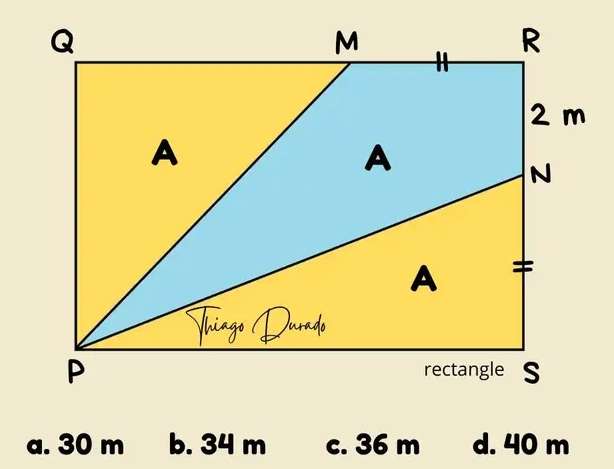
Mathematics Question and Solution
Calculating the perimeter of the rectangle (QRSP).
Let MR = NS = a
b = (2+a)
b is the width of the rectangle (RS).
Let PS = QR = c, the length of the rectangle.
It implies;
½*ac = A
ac = 2A
c = (2A/a) m.
d = 3A
d is the area of the ascribed rectangle (QRSP).
Therefore;
c*b = d
(2A/a)*(2+a) = 3A
4A+2Aa = 3Aa
4A = Aa
a = 4 m.
Again, a is MR = NS.
Recall.
b = (2+a)
And a = 4 m.
b = 2+4
b = 6 m.
b is RS, the width of the rectangle.
Calculating c, length of the rectangle.
½(c-a)6 = A
½(c-4)6 = A
3c-12 = A --- (1).
½*c*a = A
½*c*4 = A
2c = A --- (2).
Equating (1) and (2).
3c-12 = 2c
c = 12 m.
Again, c is the length of the rectangle.
It implies;
Perimeter of the rectangle (QRSP) is;
2c+2b
= 2(12)+2(6)
= 24+12
= 36 m.