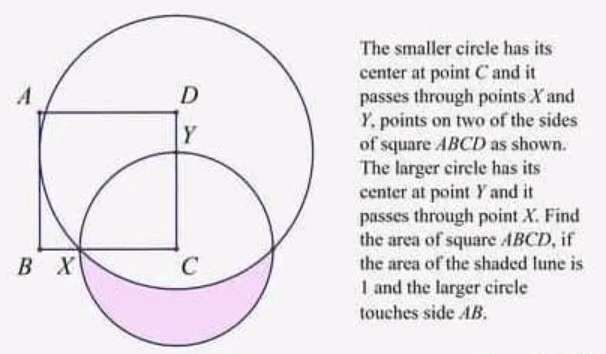
Mathematics Question and Solution
Let YC, radius of the small circle be r.
Notice;
XY = CD = AD = AB = BC = single side length of square ABCD.
Calculating r.
πr² - ½(πr²) - 90π(XY)²/360 + ½(XY)² = 1
XY will be;
√(r²+r²) = √(2r²)
XY = √(2)r
Therefore;
πr² - ½(πr²) - π(√(2)r)²/4 + ½(√(2)r)² = 1
2πr² - πr² - πr² + 2r² = 2
2r² = 2
r² = 1
r (radius of the small circle) is;
r = 1 unit.
Therefore;
XY = CD = AD = AB = BC = √(2)r
And r = 1
XY = CD = AD = AB = BC = √(2) unit.
Therefore area square ABCD is;
√(2)²
= 2 square units.