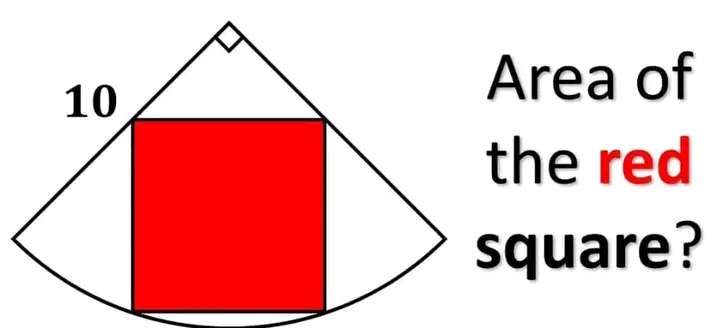
Mathematics Question and Solution
Let the side length of the inscribed square be a.
Calculating the area of the inscribed red square.
2b² = a²
b = ½√(2)a unit.
c² = 2a²
c = √(2)a unit.
c is the diagonal of the inscribed red square.
It implies;
10² = (½√(2)a)²+(√(2)a)²
100 = (a²/2)+2a²
100 = ½(5a²)
5a² = 200
a² = 40
a = 2√(10) units.
Therefore, area red inscribed square is;
a² = 40 square units.
Again, a = 2√(10) units is the side length of the inscribed red square.