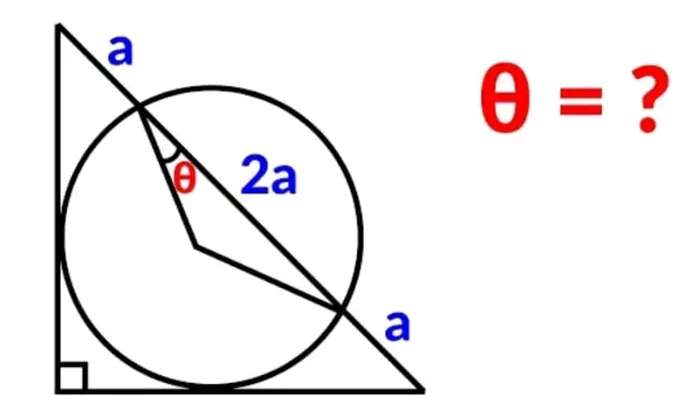
Mathematics Question and Solution
Let a be 1 unit.
b = 1+(2*1)+1
b = 4 units.
c = ½(b)
c = 2 units.
2d² = 4²
d² = 8
d = 2√(2) units.
e² = 1²+(2√(2))²-2*2√(2)cos45
e = √(9-4)
e = √(5) units.
(√(5)/sin45) = (1/sinf)
f = 18.4349488229°
g = 90-2f
g = 53.1301023542°
h = ½(g)
h = 26.5650511771°
J² = 2k²
j = √(2)k units.
k is the radius of the circle.
l = (2-√(2)k) units.
k² = 1²+(2-√(2)k)²
k² = 1+4-4√(2)k+2k²
k²-4√(2)k+5 = 0
Calculating k via completing the square approach.
(k-2√(2))² = -5+(-2√(2))²
(k-2√(2))² = -5+8
(k-2√(2))² = 3
k = 2√(2)±√(3)
It implies;
k = (2√(2)-√(3)) units.
k = 1.0963763172 units.
Again, k is the radius of the circle.
Therefore;
l = (2-√(2)k)
And k = 1.0963763172
units.
l = 2-√(2)*1.0963763172
l = 0.4494897428 units.
Calculating the required angle theta.
Let it be m.
tanm = 0.4494897428/1
m = atan(0.4494897428)
m = 24.2034283378°
Again, m is the required angle theta