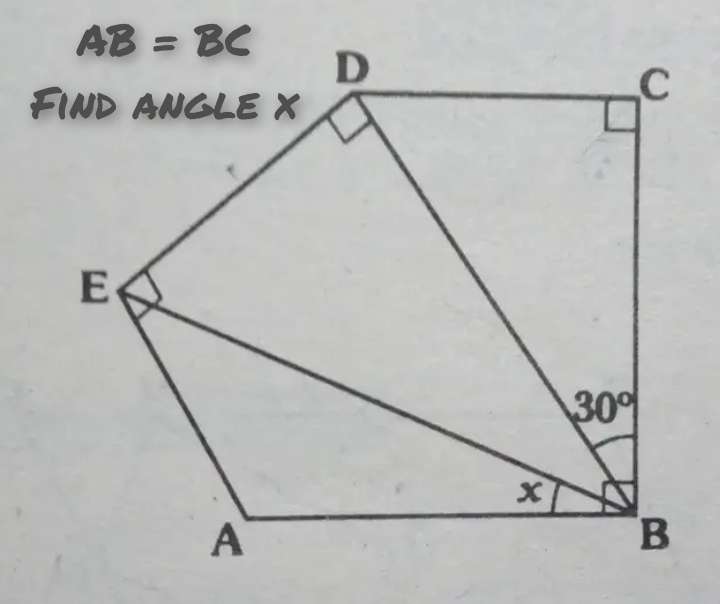
Mathematics Question and Solution
Let AB = BC = 1 unit.
tan30 = a/1
a = ⅓√(3) units.
a = 0.5773502692 units.
a is CD.
cos30 = 1/b
b = ⅓(2√(3)) units.
b = 1.1547005384 units.
b is BD.
c = 90-30
c = 60°
c is angle BDC.
3(90)+90+60+d = 180(5-2)
270+150+d = 540
540° is the sum of the interior angles of the irregular pentagon ABCDE.
d = 540-270-150
d = 540-420
d = 120°
d is angle BAE.
e = 90-30
e = 60°
e is angle ABD.
f² = 1.1547005384²+1-2*1.1547005384cos60
f = 1.0856485596 units.
f is AD.
(1.0856485596/sin60) = (1/sing)
g = 52.9113369181°
g is angle ADB.
h = 90-g
h = 37.0886630819°
h is angle ADE.
sinh = j/f
1.0856485596sin37.0886630819 = j
j = 0.6547005384 units.
j is AE.
k² = 0.6547005384²+1-2*0.6547005384cos120
k = 1.443375673 units.
k is BE.
Therefore, the required angle x (angle ABE) is;
(0.6547005384/sinx) = (1.443375673/sin120)
sinx = (0.6547005384sin120)/1.443375673
sinx = 0.392820323
x = asin(0.392820323)
x = 23.1301023547°
Again, x is the required angle (angle ABE).