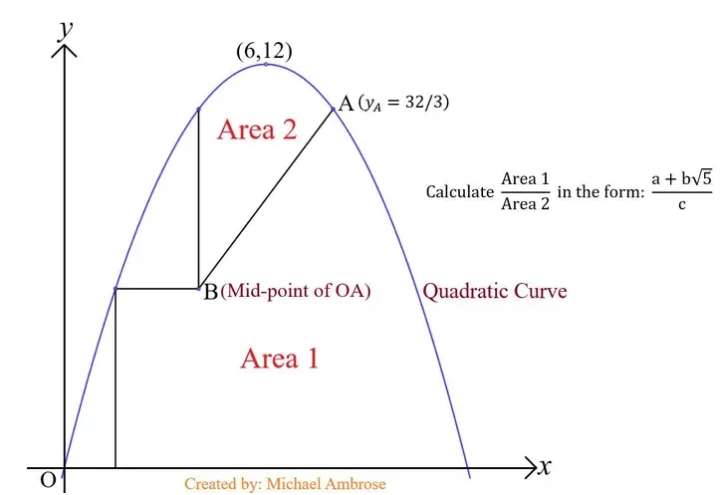
Mathematics Question and Solution
Calculating equation of the curve.
(y-12) = a(x-6)²
At x = 0, y = 0
Calculating a.
-12 = a*36
a = -⅓
It implies;
y-12 = -⅓(x-6)²
y = -⅓(x²-12x+36)+12
y = ⅓(-x²+12x-36+36)
y = ⅓(12x-x²)
Where y = ⅓(12x-x²) is the equation of the curve.
Calculating x when y = (32/3).
(32/3) = = ⅓(12x-x²)
32 = 12x-x²
x²-12x+32 = 0
Calculating x via completing the square approach.
(x-6)² = -32+36
x = 6±√(4)
x ≠ 6-2
x = 6+2
x = 8 units.
Calculating x when y = 0.
0 = ⅓(12x-x²)
x² = 12x
x = 12 units.
b = ½(32/3)
b = (16/3) units.
b is y coordinate.
Calculating x when y = 16/3 units.
(16/3) = ⅓(12x-x²)
x²-12x+16 = 0
Calculating x via completing the square approach.
(x-6)² = -16+36
x = 6±√(20)
x = 6±√(2√(5))
x ≠ (6+2√(5))
x = (6-2√(5)) units.
c = 4-(6-2√(5))
c = (2√(5)-2) units.
Area 2 is;
(Area under the curve at x = 4 and x = 8) - Area quadrilateral with parallel sides (16/3) units and (32/3) units respectively, and height 4 units.
⅑(416)-½((16/3)+(32/3)))*4)
⅑(416)-2(48/3)
⅑(416)-32
= ⅑(128) square units.
Area 1 is;
(Area under the curve at x = 4 and x = 12) + Area rectangle with length (16/3) units and width (2√(5)-2) units - Area 1
= ⅑(640)+((16/3)*(2√(5)-2))-⅑(128)
= ⅑(512)+⅓(32√(5)-32)
= ⅑(512+96√(5)-96)
= ⅑(416+96√(5)) square units.
Therefore;
Area 1 ÷ Area 2 in the form (a+b√(5))/c is;
⅑(416+96√(5))÷⅑(128)
= (416+96√(5))/128
= ¼(13+3√(5))
= 4.92705