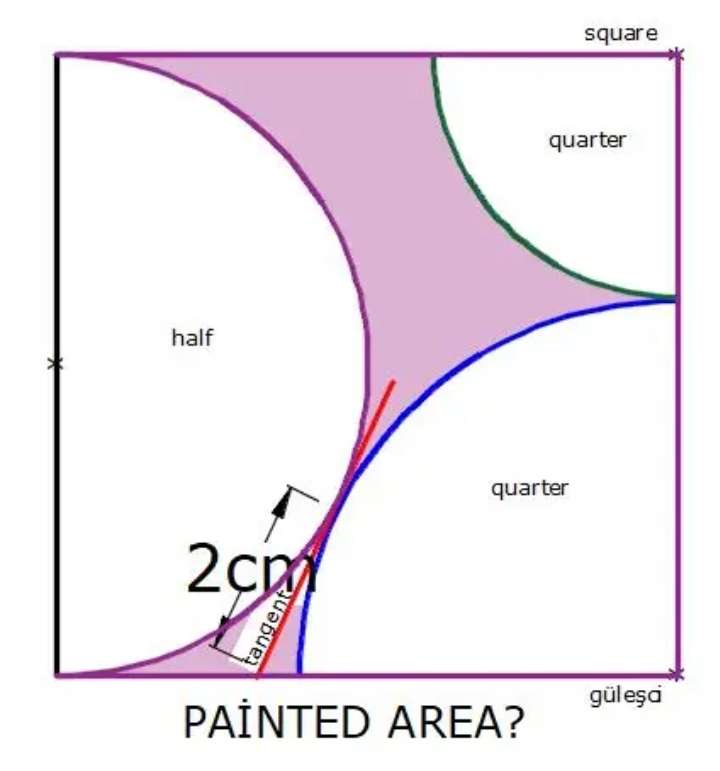
Mathematics Question and Solution
Let the square side be 2a cm.
It implies;
a is the radius of the inscribed semi circle.
Let b equal the radius of the big inscribed quarter circle.
Therefore;
(a+b)² = a²+(2a)²
a²+2ab+b² = 5a²
2ab+b² = 4a² --- (1).
(2a-2)² = 2²+b²
4a²-8a+4 = 4+b²
b² = 4a²-8a --- (2)
From (2).
b = √(4a²-8a) --- (3).
Substituting (2) and (3) in (1) to get a.
2ab+b² = 4a²
2a√(4a²-8a)+4a²-8a = 4a²
2a√(4a²-8a) = 8a
4a²(4a²-8a) = 64a²
4a²-8a = 16
a²-2a-4 = 0
Resolving the above quadratic equation via completing the square approach to get a.
(a-1)² = 5
a = 1±√(5)
It implies;
a ≠ 1-√(5)
a = (1+√(5)) cm.
a = 3.2360679775 cm.
Again, a is the radius of the inscribed semi circle.
Therefore, the square side length, 2a is;
2a = 2(1+√(5)) cm
= 6.472135955 cm.
At (3).
b = √(4a²-8a)
And a = (1+√(5)) cm.
b = √(4(1+√(5))²-8(1+√(5)))
b = 4 cm.
Again, b is the radius of the big inscribed quarter circle.
Let c be the radius of the small inscribed quarter circle.
Calculating c.
c+b = 2a
c+4 = 2(1+√(5))
c = 2+2√(5)-4
c = (2√(5)-2) cm.
Again, c is the radius of the small inscribed quarter circle.
Painted Area is;
Area square with side (2+2√(5)) cm - Area half circle with radius (1+√(5)) cm - Area quarter circle with radius 4 cm - Area quarter circle with radius (2√(5)-2) cm.
= (2+2√(5))²-½(1+√(5))²π-¼(4)²π-¼(2√(5)-2)²π
= 24+8√(5)-½(6+2√(5))π-¼(16)π-¼(24-8√(5))π
= 24+8√(5)-3π-√(5)π-4π-6π+2√(5)π
= 24+8√(5)-13π+√(5)π
= 24+8√(5)-(13-√(5))π cm²
= 8.0726540544 cm²