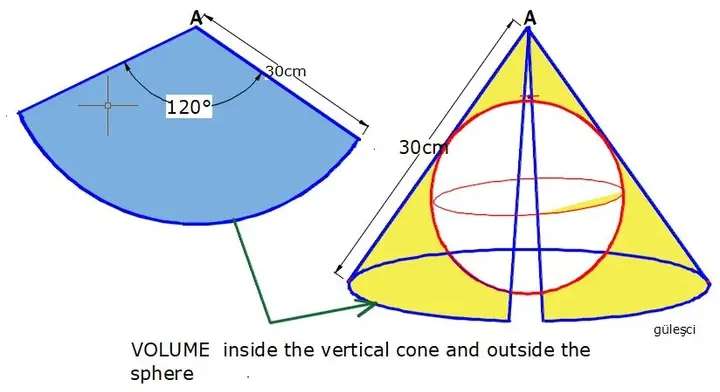
Mathematics Question and Solution
a = 120π*2*30÷360
a = ⅓(60)π
a = 20π cm.
a = 62.8318530718 cm.
a is the length of arc of the sector and also, the base circumference of the cone.
20π = 2πb
b = 10 cm.
b is the radius of the base of the circular cone.
30² = 10²+c²
c² = 900-100
c = √(800)
c = 20√(2) cm.
c is the height of the cone.
Volume of the cone is;
⅓*10*10π*20√(2)
= ⅓(2000√(2))π cm³
= 2961.9219587722 cm³
Calculating the volume outside the sphere.
2*30d+20d = 20*20√(2)
80d = 400√(2)
d = 5√(2) cm.
d is the radius of the inscribed sphere.
Sphere volume is;
⅓*4π(5√(2))³
= ⅓(1000√(2))π cm³
It implies, volume outside the sphere in the cone is;
Cone volume - Sphere volume
= ⅓(2000√(2))π-⅓(1000√(2))π
= ⅓(1000√(2)π) cm³