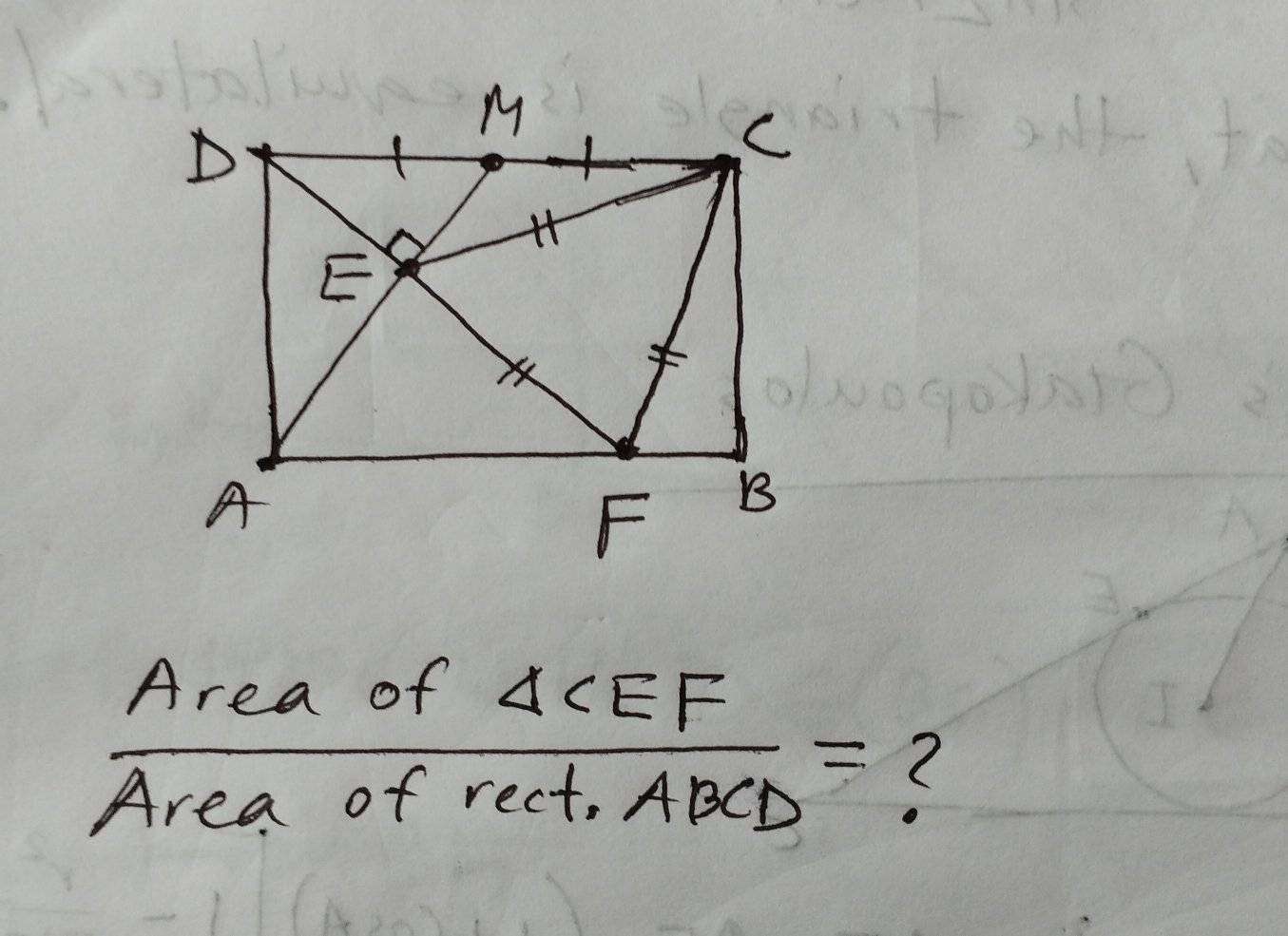Mathematics Question and Solution
Let AB be 4 units.
Let BC be 3 units.
Area ABCD is;
4*3 = 12 square units.
Calculating Area CEF.
tana = 3/2
a = atan(3/2)°
a is angle AMD.
b = atan(2/3)°
b is angle DEM.
c = (180-atan(3/2))°
c is angle CME.
sin(atan(2/3)) = d/2
d = 4√(13)/13 units.
d is EM.
e² = (4√(13)/13)²+2²-4*(4√(13)/3)sin(180-atan(3/2))
e = 10√(13)/13 units.
e is side length of the inscribed regular triangle.
Area CEF is;
0.5*(10√(13)/13)²*sin60
= 0.5*(100/13)*(√(3)/2)
= 25√(3)/13 square units.
Area Triangle CEF ÷ Area Rectangle ABCD is;
(25√(3)/13)÷12
= 25√(3)/156
= 0.2775722448