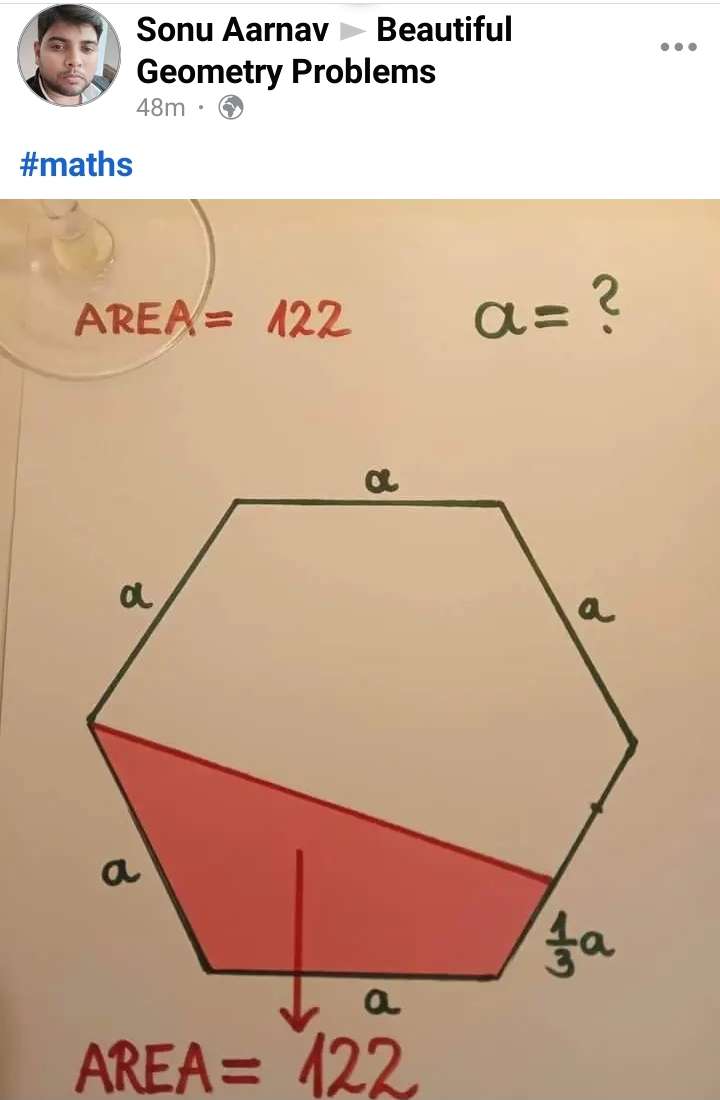
Mathematics Question and Solution
Calculating a, side length of the regular hexagon.
Notice;
Red Area is 122 square units.
sin30 = b/a
b = (a/2) units.
c = a+2b
c = 2a units.
sin60 = d/a
d = (√(3)a/2) units.
It implies;
122+0.5*2a*(2a/3)sin60 = 0.5(a+2a)(√(3)a/2)
122+⅓(√(3)a²) = ¼(3√(3))a²
122 = ¼(3√(3))a²-⅓(√(3)a²)
122 = (5√(3)a²)/12
1464 = 5√(3)a²
a² = 1464/(5√(3))
a = √(169.04815881872)
a = 13.00185213032 units.
≈ 13 units to the nearest whole number.