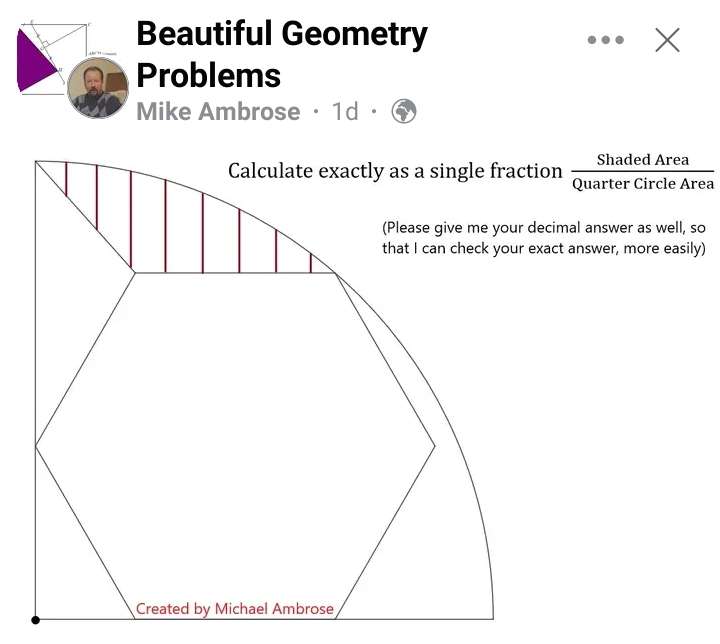
Mathematics Question and Solution
Let the inscribed regular hexagon side length be 1 unit.
a² = 2-2cos120
a = √(3) units.
sin30 = b/1
b = ½ units.
c = 1+b
c = (3/2) units
Calculating r, radius of the ascribed quarter circle.
r² = (3/2)²+√(3)²
r² = (9/4)+3
r = √(21/4)
r = ½√(21) units.
Area quarter circle is;
¼(½√(21))²π
= (21π/16) square units.
= 4.12334035784 square units.
Calculating the shade area.
tand = √(3)/(3/2)
d = atan(2√(3)/3)°
e = 90-d
e = (90-atan(2√(3)/3)))°
f² = √(3)²+(½)²
f² = 3+¼
f = √(13/4)
f = ½√(13) units.
tang =√(3)/(1/2)
g = atan(2√(3))°
h = 90-g
h = (90-atan(2√(3)))°
j = 180-g
j = (180-atan(2√(3)))°
Therefore;
Shaded Area exactly in decimal is;
Area sector with radius ½√(21) units and angle (90-atan(2√(3)/3)))° - Area triangle with base ½√(21) units and height ½√(13)sin(90-atan(2√(3))) units - Area triangle with base ½√(13) units and height sin(180-atan(2√(3))) units.
= (90-atan(2√(3)/3)))π(½√(21))²/360 - 0.5*½√(21)*½√(13)sin(90-atan(2√(3))) - 0.5*½√(13)sin(180-atan(2√(3)))
= 1.87352649473-0.57282196187-0.86602540378
= 0.43467912908 square units.
It implies;
Shade Area ÷ Area Quarter Circle is;
0.43467912908÷4.12334035784
= 0.10541917265
≈ 0.11 to 2 decimal places.