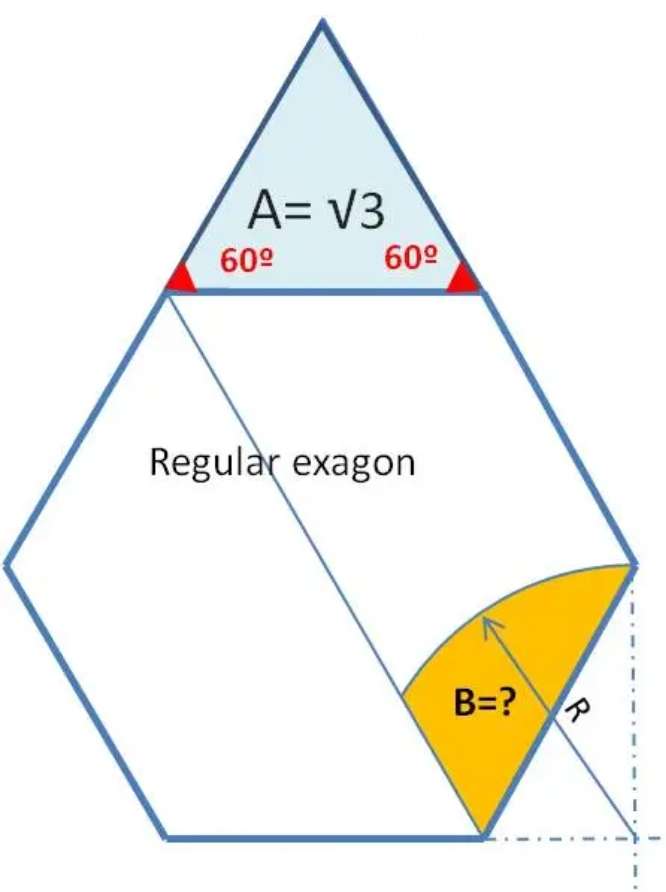
Mathematics Question and Solution
Let a be the side length of regular hexagon and the regular triangle (equilateral triangle).
Calculating a.
0.5a²sin60 = √(3)
¼*√(3)a² = √(3)
¼(a²) = 1
a² = 4
a = 2 units.
Again, a is the side length of the regular hexagon and the regular triangle (equilateral triangle).
sin60 = b/2
b = √(3) units.
b is R, radius of the arc.
cos60 = c/2
c = 1 unit.
(1/sind) = (√(3)/sin120)
d = 30°
c = 90-d
c = 60°
Calculating area B (yellow inscribed area).
It implies;
Area B (yellow area) is;
Area triangle with height 1 unit and base sin120 units + Area sector with radius √(3) units and angle 60° - Area triangle with height √(3) units and base 1 unit.
= 0.5sin120+(60π*√(3)²÷360)-0.5*√(3)
= ¼√(3)+½(π)-½√(3)
= ¼(√(3)+2π-2√(3))
= ¼(2π-√(3)) square units.
= 1.1377836249 square units.