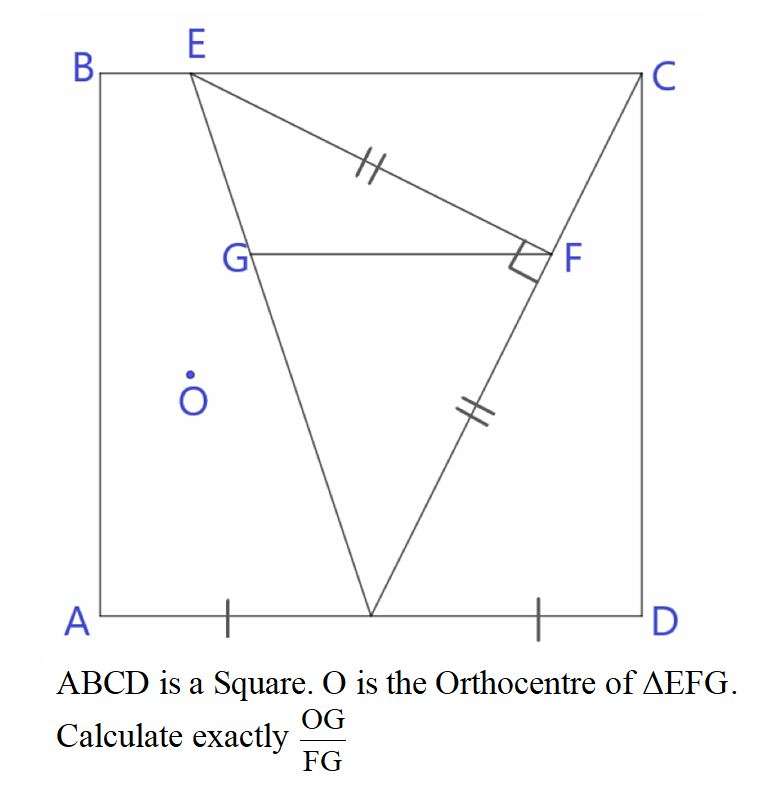
Mathematics Question and Solution
Sir Mike Ambrose is the author of the question.
Let the two equal length be 2 units each.
2 = 2/a
a = 1 unit.
sin(atan(½)) = b/3
b = ⅕(3√(5)) units.
c = 2b
c = ⅕(6√(5)) units.
Where c is the square side.
d² = 2²+1²
d = √(5) units.
e = ⅕(6√(5))-d
e = ⅕(√(5)) unit.
sin(atan2) = f/1
f = ⅕(2√(5)) units.
cos(atan2) = g/1
g = ⅕(√(5)) unit.
h = ⅕(3√(5))-⅕(√(5))
h = ⅕(2√(5)) units.
3 = (⅕(2√(5)))/i
i = (2√(5))/15 unit.
Therefore;
Length FG exactly is;
d-g-i
= √(5)-⅕(√(5))-(2√(5))/15
= ⅓(2√(5)) units.
Calculating length OG.
cos(atan½) = j/(⅓(2√(5)))
j = ⅓(4) units.
sin(atan½) = k/(⅓(2√(5)))
k = ⅔ units.
tan(45+atan(⅓)) = l/(⅔)
2 = 3l/2
3l = 4
l = ⅓(4) units.
Therefore;
Length OG is;
l - k
= ⅓(4)-(⅔)
= ⅔ units.
It implies;
OG ÷ FG exactly is;
(⅔) ÷ (⅓(2√(5)))
= ⅕(√(5)).