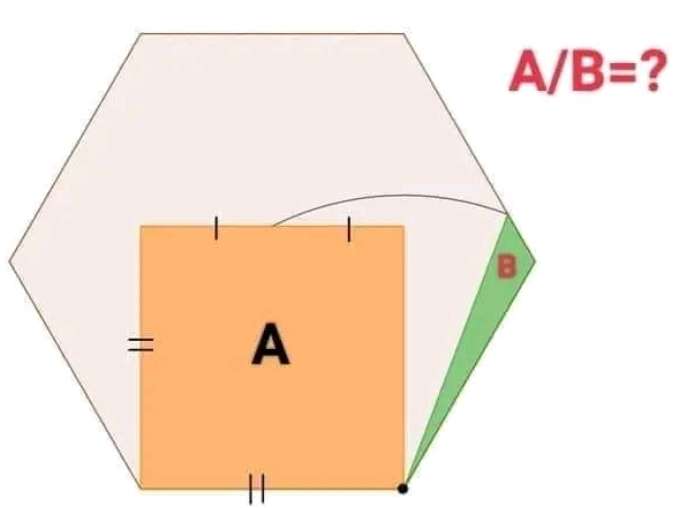
Mathematics Question and Solution
Let the side length of the regular hexagon be 1 unit.
Therefore, area A (area inscribed square) is;
1²
= 1 square unit.
Calculating area B.
a² = 1²+(½)²
a² = 1+¼
a = √(5/4)
a = ½√(5) units.
a = 1.1180339887 units.
a is the radius of the inscribed arc.
b = ⅙*180(6-2)
b = 120°
b is the single interior angle of the regular hexagon.
It implies;
(½√(5)/sin120) = (1/sinc)
c = 50.7684795195°
d = 60-c
d = 9.2315204805°
Area B is;
0.5*1.1180339887sin9.2315204805
= 0.0896798669 square units.
Therefore;
Area A ÷ Area B is ;
1÷0.0896798669
= 11.1507748052