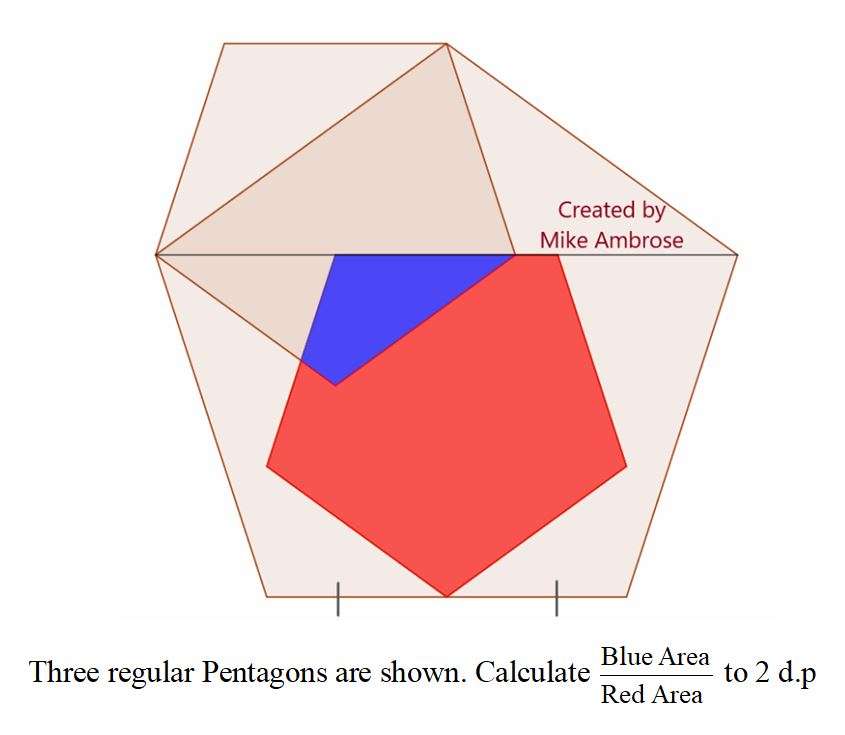
Mathematics Question and Solution
Let the biggest regular pentagon side length be 2 units.
sin72 = a/2
a = 1.90211303259 units.
tan72 = (1.90211303259/b)
b = 0.61803398875 unit.
c = 2b
c = 1.2360679775 units.
Where c is the side length of the regular red and blue pentagon.
Calculating area of the regular red and blue pentagon.
(5*1.2360679775²)/(4tan36)
= 2.6286555606 square units.
d² = 8-8cos108
d = 3.2360679775 units.
e = ½(3.2360679775-c)
e = 1 unit.
f² = 8-8cos36
f = 1.2360679775 units.
g² = 2-2cos36
g = 0.61803398875 unit.
Area Blue is;
(0.5(1.2360679775²)sin108) - (0.5(sin36))
= 0.72654252801 - 0.29389262615
= 0.43264990186 square units.
Therefore;
Area Red is;
2.6286555606 - 0.43264990186
= 2.19600565874 square units.
It implies;
Area Blue ÷ Area Red to 2 decimal places is;
0.43264990186 ÷ 2.19600565874
= 0.19701675182
≈ 0.2