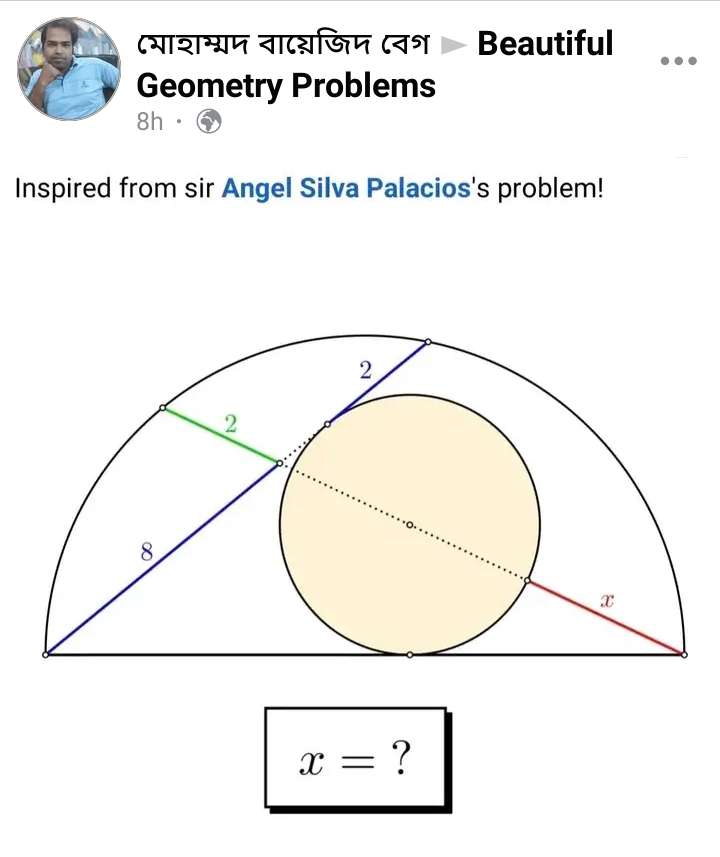
Mathematics Question and Solution
a² = 8²-2²
a = √(60)
a = 2√(15) units.
Let the radius of the inscribed circle be r.
Considering similar triangle ratios, calculating r.
r = 2√(15)
1 = 2
Cross Multiply.
r = √(15) units.
b² = 1+r²
b² = 1+√(15)²
b = √(16)
b = 4 units.
c = 2+4+√(15)+x
c = (6+√(15)+x) units.
d² = (x+√(15))²-√(15)²
d² = x²+2√(15)x+15-15
d = √(x²+2√(15)x)
Again, considering similar triangle ratios to get x.
√(15) = 2√(15)
√(x²+2√(15)x) = (6+√(15)+x)
Cross Multiply
√(15)(6+√(15)+x) = 2√(15)*√(x²+2√(15)x)
(6√(15)+15+√(15)x)² = 60(x²+2√(15)x)
(38.23790007724+3.87298334621x)² = 60x²+464.75800154489x
1462.13700231734+296.18950038622x+15x² = 60x²+464.75800154489x
45x²+168.56850115867x-1462.13700231734 = 0
Solving The quadratic equation.
x = 4.12702 units.