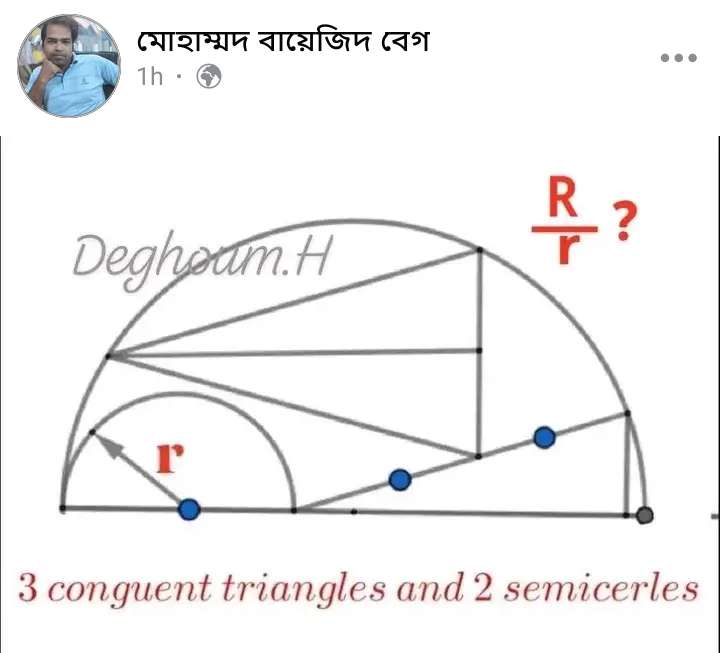
Mathematics Question and Solution
Let r = 1 units.
Let the ascribed half circle's radius be x.
Therefore;
a = (x-2) units.
b = ½(x-2) units.
c = x-b
c = x-½(x-2)
c = ½(x+2) units.
d = 2a
d = 2(x-2)
d = (2x-4) units.
Therefore
x² = c²+d²
x² = (½(x+2))²+(2x-4)²
x² = ¼(x²+4x+4)+4x²-16x+16
4x² = x²+4x+4+16x²-64x+64
13x²-60x+68 = 0
Therefore, solving the quadratic equation.
x ≠ 2 units.
x = (34/13) units.
x = 2.61538461538 units.
Where x is the radius of the ascribed half circle (R).
Notice, r , radius of the inscribed small half circle is 1 unit.
It implies;
R ÷ r is;
(34/13)÷1
= (34/13)
= 2.61538461538