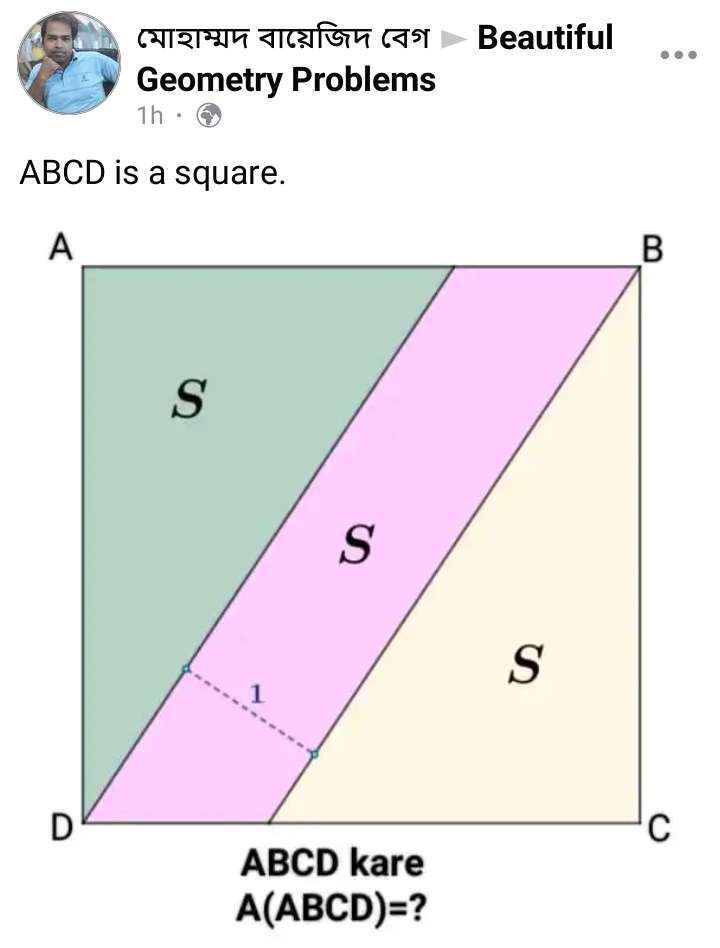
Mathematics Question and Solution
Let the side length of square ABCD be a.
Area Square ABCD will be a²
Calculating a²
Notice, he three inscribed plane shapes, two congruent right-angled triangle and a parallelogram has equal area.
Therefore;
½(3ab) = a²
b = (2a/3) --- (1).
Where b is the base length of the two congruent inscribed right-angled triangle.
ab + √(a²+b²) = a² --- (2).
Substituting (1) in (2).
a(2a/3) + √(a²+(2a/3)²) = a²
(2a²/3)+√(a²+(4a²/9)) = a²
(13a²/9) = (a²/3)²
(13a²/9) = (a⁴/9)
13 = a²
a² is the area of Square ABCD.