Mathematics Question and Solution
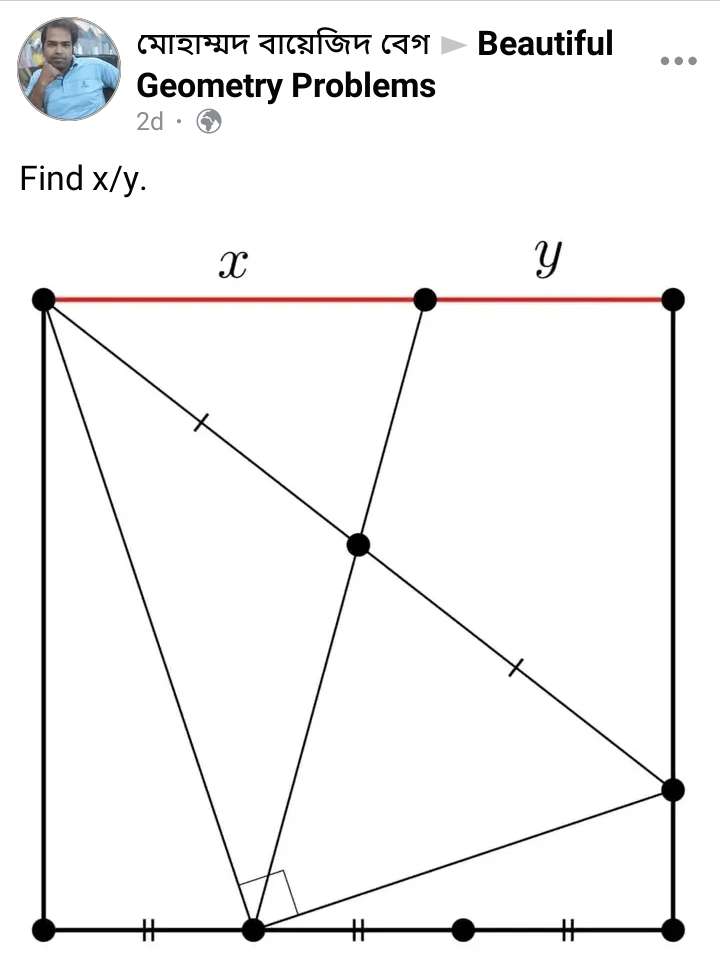
Let the square side be 3 cm.
Therefore;
Observing similar triangle ratios.
3 = 2
1 = a
Cross Multiply.
a = ⅔ units.
b = √(3²+1²)
b = √(10) cm.
c = √(2²+(⅔)²)
c = ⅓(2√(10)) cm.
d = √(√(10)²+(⅓(2√(10)))²)
d = ⅓√(130) cm.
e =½(d)
e = ⅙√(130) cm.
tanf = (√(10)/(2√(10)/3))
f = 56.30993247402°
g = 180-56.30993247402-atan(2/(2/3))
g = 52.1250163489°
h = 90-52.1250163489
h = 37.8749836511°
j² = (⅙√(130))²+(⅓(2√(10)))²-2(⅙√(130))(½(2√(10)))cos56.30993247402
j = 1.90029237517 cm.
(1.90029237517/sin56.30993247402) = ((2√(10)/3)/sink)
k = 67.38013505196°
l = 180-67.38013505196-37.8749836511
l = 74.74488129694°
Calculating x.
(x/sin67.38013505196) = ((√(130)/6)/sin74.74488129694)
x = 1.81818181818 cm.
x = (20/11) cm.
Therefore y is;
3-x
= 3-(20/11)
= (13/11) cm.
It implies;
x÷y is;
(20/11)÷(13/11)
= 20/13
= 1.53846153846