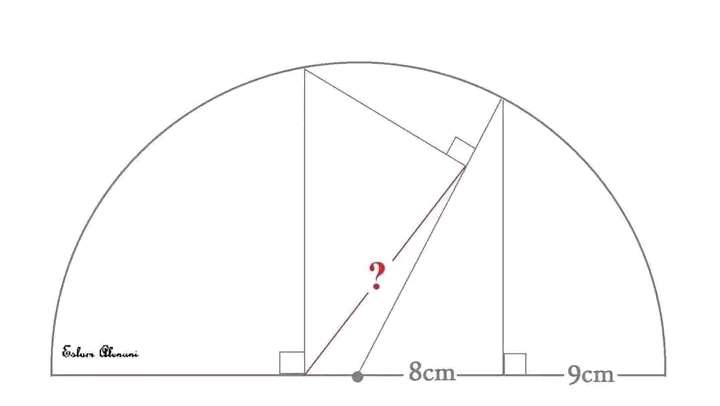
Mathematics Question and Solution
a = 8+9
a = 17 units.
a is the radius of the half circle.
b²+8² = 17²
b = √(225)
b = 15 units.
c²+d² = 17²
c = √(289-d²) units.
e = (17-d) units.
f = ½(c)
f = ½√(289-d²) unit.
g = 17+17-9
g = 34-9
g = 25 units.
Observing similar plane shape (right-angled) side length ratios.
(17-d) - 25
½√(289-d²) - 15
Cross Multiply.
15(17-d) = 25*½√(289-d²)
30(17-d) = 25√(289-d²)
6(17-d) = 5√(289-d²)
102-6d = 5√(289-d²)
(102-6d)² = 25(289-d²)
10404-1224d+36d² = 7225-25d²
11d²-1224d+3179 = 0
It implies;
d = (612-85√(47))/11 units.
d = 2.66085 units.
c = √(289-d²)
And d = 2.66085 units.
c = √(289-2.66085²)
c = 16.7904698349 units.
tanh = 15/8
h = 61.9275130641°
tanj = 16.7904698349/2.66085
j = 80.9950039608°
k = 180-j-h
k = 37.0774829751°
l² = 2(17)²-2(17)²cos37.0774829751
l = 10.8101574897 units.
m = ½(180-37.0774829751)
m = 71.4612585125°
sin71.4612585125 = n/10.8101574897
n = 10.2492063929 units.
o = 90-71.4612585125
o = 18.5387414875°
p = 90-80.9950039608
p = 9.0049960392°
q = m-o+p
q = 71.4612585125-18.5387414875+9.0049960392
q = 61.9275130642°
Therefore, the required length is;
Let it be r.
r² = 16.7904698349²+10.2492063929²-2*16.7904698349*10.2492063929cos61.9275130642
r = 15 units.
Again, r is the required length.