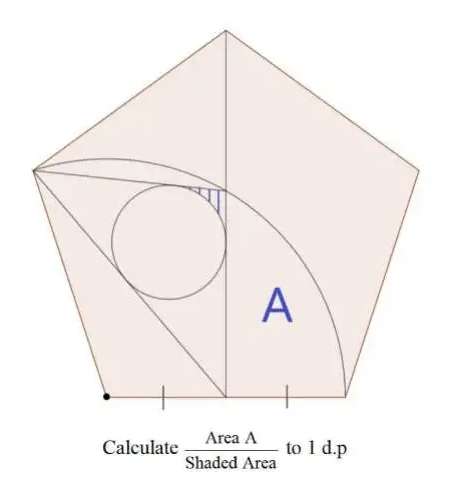
Sir Mike Ambrose is the author of the question.
Let the side length of the regular pentagon be 2 units.
a² = 2²-1²
a = √(3) units.
b² = 5-4cos108
b = 2.49721204096 units.
(2.49721204096/...
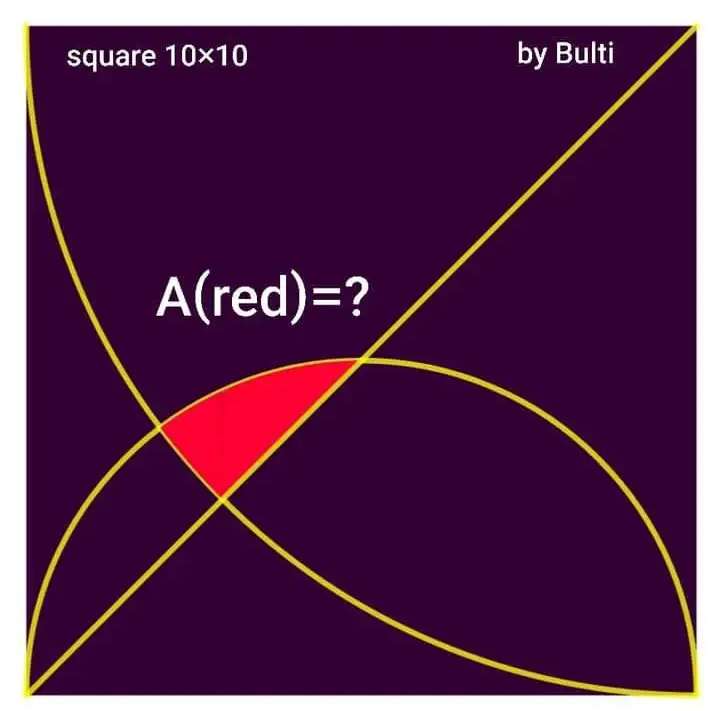
Calculating Area Red.
tana = 5/10
a = atan(½)°
b = 2a
b = 2atan(½)°
c = b-45
c = 8.1301023542°
d² =10²+10²-2*10*10cos8.1301023542
d = 1.4177804018 units.
e = ½(180-8.1301023542)
e...
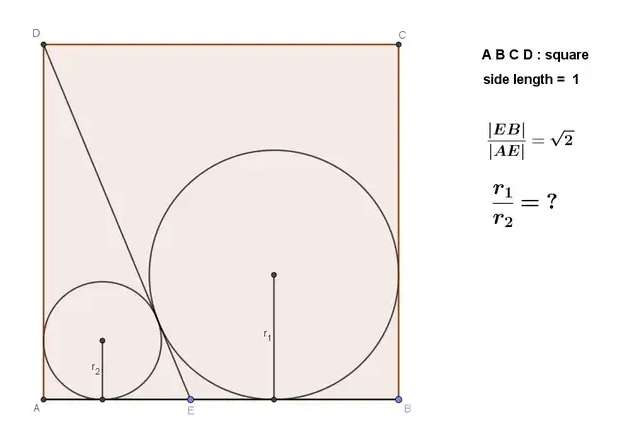
Let EB be a.
Let AE be b.
It implies;
a/b = √(2) --- (1).
a+b = 1 --- (2).
From (1).
a = √(2)b --- (3).
Substituting (3) in (2) to get b.
√(2)b+b = 1
b(√(2)+1) = 1
b = (√...
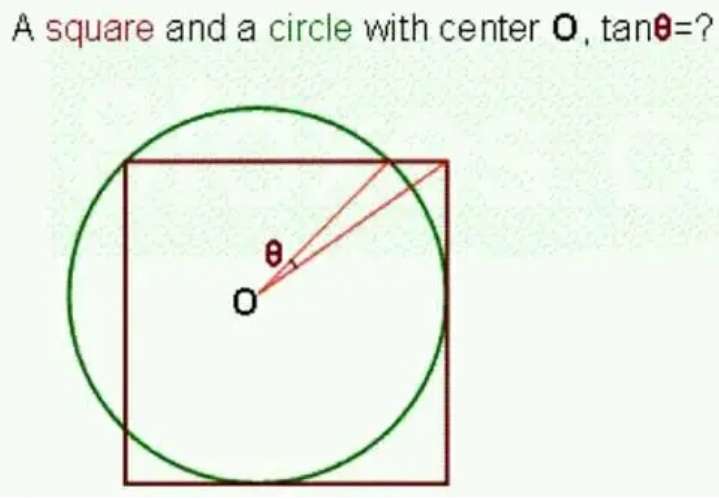
Let the radius of the circle be 2 units.
a = (2-b) units.
Calculating b.
2² = 2(2-b)²
4 = 2(4-4b+b²)
b²-4b+2 = 0
(b-2)² = -2+(-2)²
(b-2)² = 2
b = 2±√(2)
It implies;
b ≠ (2+√(2))
b...
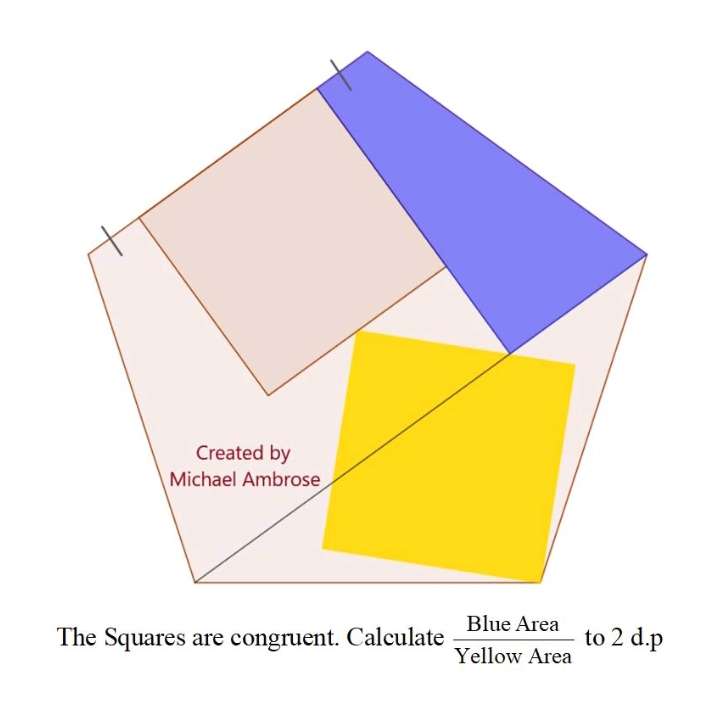
Let the regular pentagon side length be 1 unit.
sin72 = a/1
a = 0.9510565163 unit.
Let the side length of the two inscribed congruent squares be b.
c = ½(b) unit.
b+½(b) = 0.9510565163...
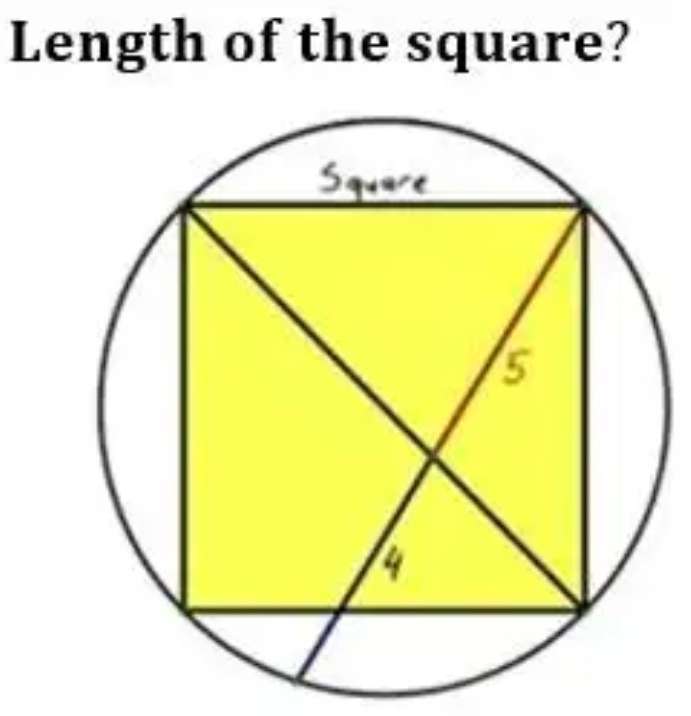
Let a be the radius of the circle.
b = 2a units.
b is the diameter of the circle.
Calculating a observing similar plane shape (right-angled triangle) ratios.
It implies;
2a - 5
9 - a...
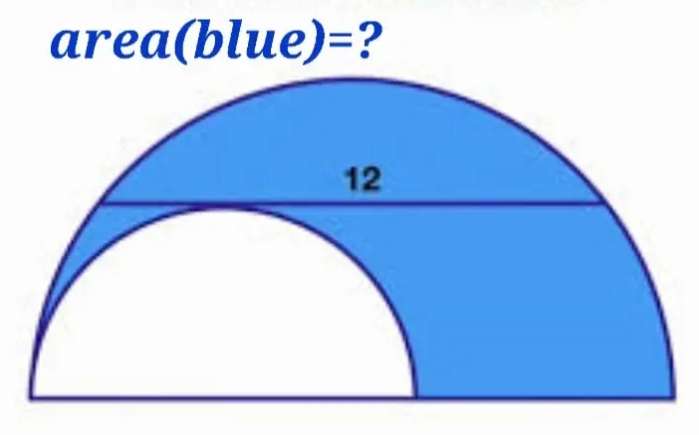
Let the radius of the ascribed half circle be a.
Let the radius of the inscribed half circle be b.
It implies;
a² = b²+(0.5*12)²
a²-b² = 6²
a²-b² = 36 square units.
Where (a²-b²) is the b...
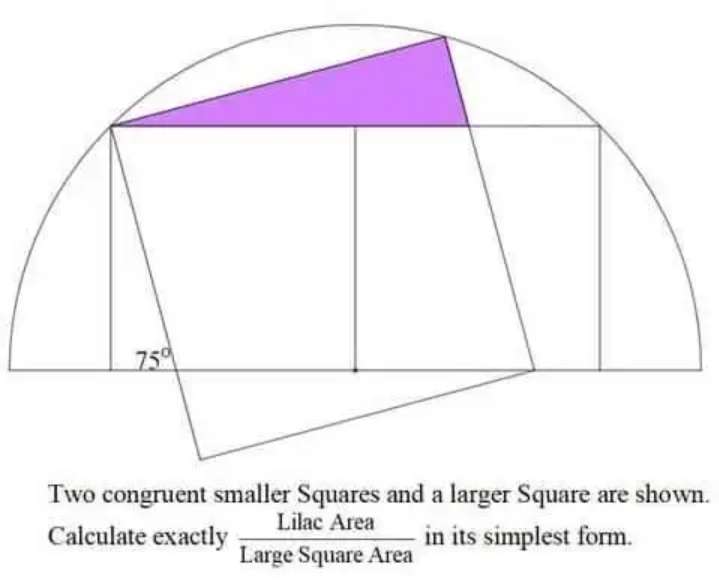
Sir Mike Ambrose is the author of the question.
Let the radius of the semi circle be 1 unit.
Therefore;
Area lilac is;
Area triangle with height 0.26794919243 units and base 1 unit
= ½(0....
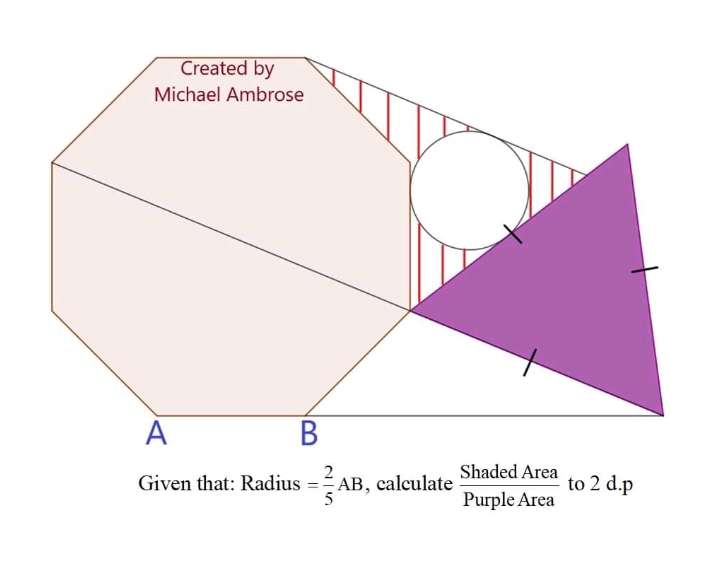
Let AB be 5 units.
Radius, r of the inscribed circle is;
5*(2/5)
r = 2 units.
a = ⅛(180*6)
a = 135°
2b² = 25
b = ½(5√(2)) units.
c = 180-0.5(135)-45
c = 67.5°
sin22.5 = ½(5√(2...
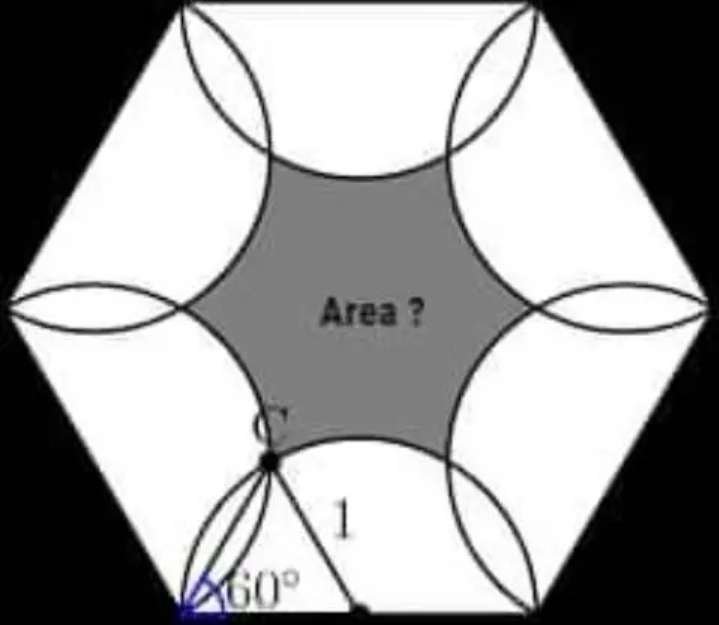
Shaded inscribed area is;
Area regular hexagon with side 1 unit - 6(Area sector with radius 1 unit and angle 60°) + 6(Area equilateral triangle with side 1 unit).
= 6/(4tan(180÷6)) - 6(60π÷36...