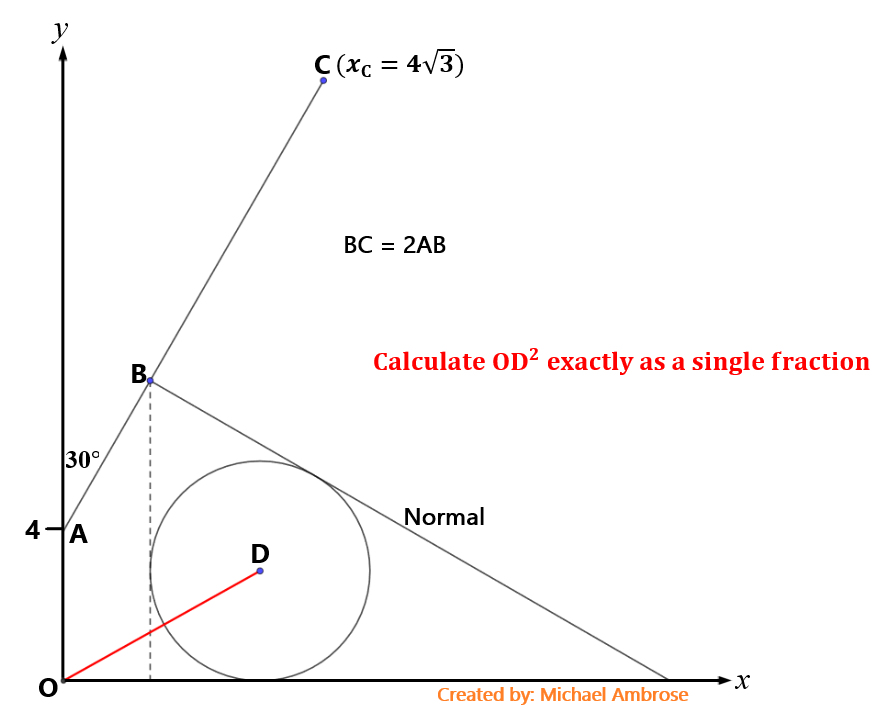
Mathematics Questions and Solution
sin30 = (4√(3))/a
a = 8√(3) units.
a is AC.
AB = ⅓(a)
AB = ⅓(8√(3)) units.
cos30 = b/⅓(8√(3))
b = ⅓(8√(3))*½√(3)
b = 4 units.
sin30 = c/⅓(8√(3))
c = ⅓(4√(3)) units.
d = 4+b
d = 8 units.
tan60 = e/8
e = 8√(3) units.
cos60 = 8/f
f = 16 units.
Let r be the radius of the inscribed circle.
16r+8r+8√(3)r = 8*8√(3)
(24+8√(3))r = 64√(3)
r = (4√(3)-4) units.
r = 2.9282 units.
g = r+c
g = (4√(3)-4)+⅓(4√(3))
g = ⅓(12√(3)-12+4√(3))
g = ⅓(16√(3)-12) units.
It implies;
Length (OD)² exactly as a single fraction is;
(OD)² = (⅓(16√(3)-12))²+(4√(3)-4)²
(OD)² = ⅓(496-224√(3)) square units.
(OD)² = 36.0068730349 square units exactly in decimal.