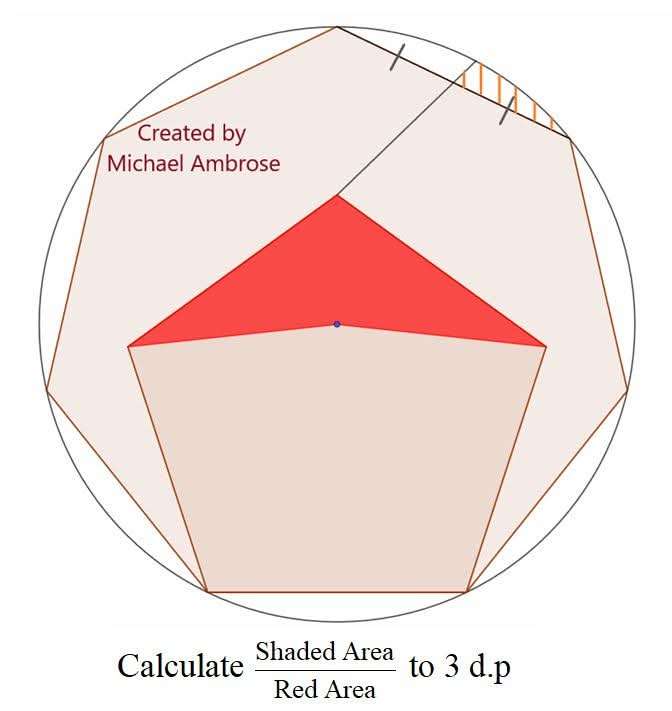
Mathematics Question and Solution
Let the side of the regular pentagon be 1 unit.
Notice;
The regular pentagon side is equal the regular heptagon side.
a = ⅐(180*5)
a = ⅐(900)°, the single interior angle of the regular heptagon.
b = 2a
b = ⅐(450)°
tan(⅐(450)) = c/0.5
c = 1.03826069829 units.
cos(⅐(450)) = 0.5/d
d = 1.15238243548 units.
Where d is the radius of the ascribed circle.
e = 180-⅐(900)
e = ⅐(360)°
tan18 = 0.5/f
f = 1.53884176859 units.
g² = 1.15238243548²-0.5²
g = 1.03826069828 units.
h = f-g
h = 0.50058107031 units.
Therefore;
Area Red is;
2(0.5*1*0.50058107031sin54)
= 0.40497859294 square units.
Calculating Area Shaded.
i = 1.15238243548-0.50058107031
i = 0.65180136517 units.
j² = 0.65180136517²+0.5²-0.65180136517cos(450/7)
j = 0.62613018307 units.
(0.62613018307/sin(450/7)) = (0.5/sink)
k = 46.01107610633°
l = 180-k
l = 133.98892389367°
1.15238243548² = 0.50058107031²+m²-2*0.50058107031mcos133.98892389367
m²+0.69532642774m-1.07740386965 = 0
m = 0.746994 units.
(0.746994/sinn) = (1.15238243548/sin133.98892389367)
n = 27.79927180468°
o² = 2(1.15238243548)²-2(1.15238243548)²cos27.79927180468
o = 0.5536549361 units.
p = 0.5(180-27.79927180468)
p = 76.10036409766°
Shaded Area is;
((360/7)π*1.15238243548²/360)-(0.5*1.15238243548²sin(360/7))-(27.79927180468π*1.15238243548²/360)+(0.5*1.15238243548²sin27.79927180468)-(0.5*0.5536549361*0.65180136517sin76.10036409766)+(0.5*0.5*0.65180136517sin(450/7))
= 0.59599839888-0.51913034914-0.32216180667+0.30966983106-0.02833979632
= 0.03603627781 square units.
Area Shaded ÷ Area Red to 3 decimal places is;
0.03603627781÷0.40497859294
= 0.08898316711
≈ 0.089