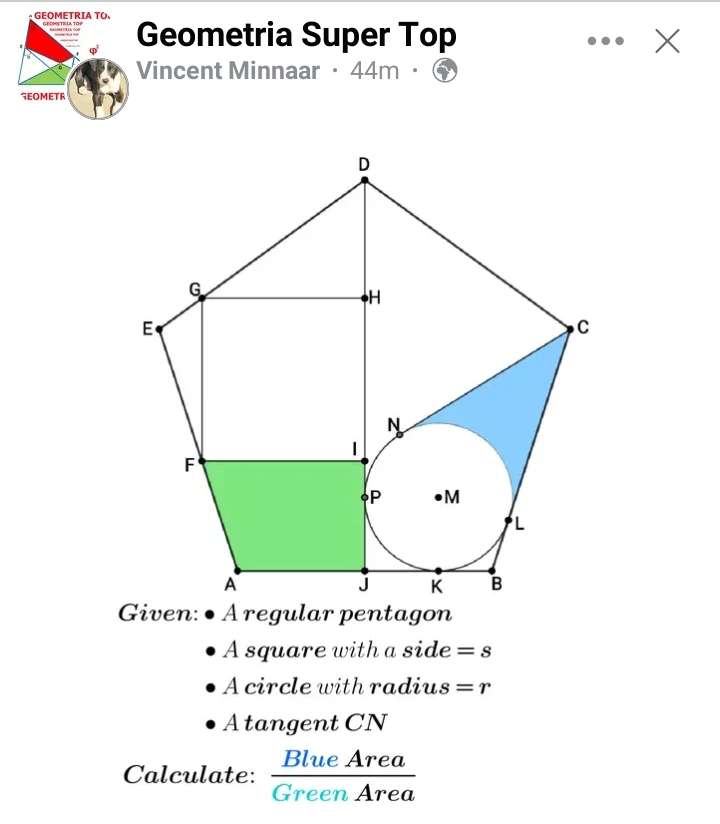
Mathematics Question and Solution
Notice;
GH = 8 units.
Calculating the side length of the regular pentagon.
a = 108-90
a = 18°
a is angle EFG.
b = 180-108-18
b = 54°
b is angle EGF.
(8/sin108) = (c/sin18)
c = 2.59935756986 units.
c is EG.
d = 90-54
d = 36°
d is angle DGH.
cos36 = 8/e
e = 9.88854382 units.
e is DG.
Therefore the regular pentagon side length (DE) is;
c+e
= 2.59935756986+9.88854382
= 12.48790138986 units.
f = ½(12.48790138986)
f = 6.24395069493 units.
f is AJ.
tan36 = g/8
g = 5.81234022404 units.
g is DH.
(h/sin108) = (12.48790138986/sin36)
h = 20.20584889695 units.
h is AD.
(DJ)² = 20.20584889695²-6.24395069493²
DJ = 19.21690426072 units.
IJ = 19.21690426072-8-5.81234022404
IJ = 5.40456403668 units.
Area Green is;
0.5(8+6.24395069493)*5.40456403668
= 0.5*14.24395069493*5.40456403668
= 38.49117183303 square units.
Calculating Area Blue.
j = 8+5.81234022404
j = 13.81234022404 units.
j is DI.
(CI)² = 13.81234022404²+12.48790138986²-2*12.48790138986*13.81234022404cos54
CI = 11.99823429641 units.
(11.99823429641/sin54) = (13.81234022404/sink)
k = 68.64443900527°
k is angle DCI.
Angle BCI is;
108-68.64443900527
= 39.35556099473°
l = ½(39.35556099473)
l = 19.67778049736°
Calculating r, radius of the inscribed circle
(r/tan19.67778049736)+(r/tan54) =
12.48790138986
3.52285068027r = 12.48790138986
r = 3.54482847082 units.
tan19.67778049736 = 3.54482847082/m
m = 9.91243275133 units.
m is CL.
n = 90-19.67778049736
n = 70.32221950264°
n is angle CML
Area Blue is;
2(0.5*9.91243275133*3.54482847082-70.32221950264*π*3.54482847082*3.54482847082÷360)
= 2*9.85758733382
= 19.71517466765 square units.
It implies;
Area Blue ÷ Area Green is;
19.71517466765÷38.49117183303
= 0.5121999079
≈0.5122 to 4 decimal places.